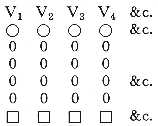
An internet resource developed by
(Return to Classics index)
Translation originally published in 1843 in the Scientific Memoirs, 3, 666-731.
(Go to the article to which the following Notes were appended)
the constants a, b, c, &c. are represented on the seven columns of discs, of which the engine consists. It can therefore tabulate accurately and to an unlimited extent, all series whose general term is comprised in the above formula; and it can also tabulate approximately between intervals of greater or less extent, all other series which are capable of tabulation by the Method of Differences.
The Analytical Engine, on the contrary, is not merely adapted for tabulating the results of one particular function and of no other, but for developing and tabulating any function whatever. In fact the engine may be described as being the material expression of any indefinite function of any degree of generality and complexity, such as for instance,
which is, it will be observed, a function of all other possible functions of any number of quantities.
In this, which we may call the neutral or zero state of the engine, it is ready to receive at any moment, by means of cards constituting a portion of its mechanism (and applied on the principle of those used in the Jacquard-loom), the impress of whatever special function we may desire to develope or to tabulate. These cards contain within themselves (in a manner explained in the Memoir itself, pages 11 and 12) the law of development of the particular function that may be under consideration, and they compel the mechanism to act accordingly in a certain corresponding order. One of the simplest cases would be, for example, to suppose that
is the particular function
which the Difference Engine tabulates for values of n only up to 7. In this case the cards would order the mechanism to go through that succession of operations which would tabulate
where n might be any number whatever.
These cards, however, have nothing to do with the regulation of the particular numerical data. They merely determine the operations[1] to be effected, which operations may of course be performed on an infinite variety of particular numerical values, and do not bring out any definite numerical results unless the numerical data of the problem have been impressed on the requisite portions of the train of mechanism. In the above example, the first essential step towards an arithmetical result would be the substitution of specific numbers for n, and for the other primitive quantities which enter into the function.
Again, let us suppose that for F we put two complete equations of the fourth degree between x and y. We must then express on the cards the law of elimination for such equations. The engine would follow out those laws, and would ultimately give the equation of one variable which results from such elimination. Various modes of elimination might be selected; and of course the cards must be made out accordingly. The following is one mode that might be adopted. The engine is able to multiply together any two functions of the form
This granted, the two equations may be arranged according to the powers of y, and the coefficients of the powers of y may be arranged according to powers of x. The elimination of y will result from the successive multiplications and subtractions of several such functions. In this, and in all other instances, as was explained above, the particular numerical data and the numerical results are determined by means and by portions of the mechanism which act quite independently of those that regulate the operations.
In studying the action of the Analytical Engine, we find that the peculiar and independent nature of the considerations which in all mathematical analysis belong to operations, as distinguished from the objects operated upon and from the results of the operations performed upon those objects, is very strikingly defined and separated.
It is well to draw attention to this point, not only because its full appreciation is essential to the attainment of any very just and adequate general comprehension of the powers and mode of action of the Analytical Engine, but also because it is one which is perhaps too little kept in view in the study of mathematical science in general. It is, however, impossible to confound it with other considerations, either when we trace the manner in which that engine attains its results, or when we prepare the data for its attainment of those results. It were much to be desired, that when mathematical processes pass through the human brain instead of through the medium of inanimate mechanism, it were equally a necessity of things that the reasonings connected with operations should hold the same just place as a clear and well-defined branch of the subject of analysis, a fundamental but yet independent ingredient in the science, which they must do in studying the engine. The confusion, the difficulties, the contradictions which, in consequence of a want of accurate distinctions in this particular, have up to even a recent period encumbered mathematics in all those branches involving the consideration of negative and impossible quantities, will at once occur to the reader who is at all versed in this science, and would alone suffice to justify dwelling somewhat on the point, in connexion with any subject so peculiarly fitted to give forcible illustration of it as the Analytical Engine. It may be desirable to explain, that by the word operation, we mean any process which alters the mutual relation of two or more things, be this relation of what kind it may. This is the most general definition, and would include all subjects in the universe. In abstract mathematics, of course operations alter those particular relations which are involved in the considerations of number and space, and the results of operations are those peculiar results which correspond to the nature of the subjects of operation. But the science of operations, as derived from mathematics more especially, is a science of itself, and has its own abstract truth and value; just as logic has its own peculiar truth and value, independently of the subjects to which we may apply its reasonings and processes. Those who are accustomed to some of the more modern views of the above subject, will know that a few fundamental relations being true, certain other combinations of relations must of necessity follow; combinations unlimited in variety and extent if the deductions from the primary relations be carried on far enough. They will also be aware that one main reason why the separate nature of the science of operations has been little felt, and in general little dwelt on, is the shifting meaning of many of the symbols used in mathematical notation. First, the symbols of operation are frequently also the symbols of the results of operations. We may say that these symbols are apt to have both a retrospective and a prospective signification. They may signify either relations that are the consequence of a series of processes already performed, or relations that are yet to be effected through certain processes. Secondly, figures, the symbols of numerical magnitude, are frequently also the symbols of operations, as when they are the indices of powers. Wherever terms have a shifting meaning, independent sets of considerations are liable to become complicated together, and reasonings and results are frequently falsified. Now in the Analytical Engine, the operations which come under the first of the above heads are ordered and combined by means of a notation and of a train of mechanism which belongs exclusively to themselves; and with respect to the second head, whenever numbers meaning operations and not quantities (such as the indices of powers) are inscribed on any column or set of columns, those columns immediately act in a wholly separate and independent manner, becoming connected with the operating mechanism exclusively, and re-acting upon this. They never come into combination with numbers upon any other columns meaning quantities; though, of course, if there are numbers meaning operations upon n columns, these may combine amongst each other, and will often be required to do so, just as numbers meaning quantities combine with each other in any variety. It might have been arranged that all numbers meaning operations should have appeared on some separate portion of the engine from that which presents numerical quantities; but the present mode is in some cases more simple, and offers in reality quite as much distinctness when understood.
The operating mechanism can even be thrown into action independently of any object to operate upon (although of course no result could then be developed). Again, it might act upon other things besides number, were objects found whose mutual fundamental relations could be expressed by those of the abstract science of operations, and which should be also susceptible of adaptations to the action of the operating notation and mechanism of the engine. Supposing, for instance, that the fundamental relations of pitched sounds in the science of harmony and of musical composition were susceptible of such expression and adaptations, the engine might compose elaborate and scientific pieces of music of any degree of complexity or extent.
The Analytical Engine is an embodying of the science of operations, constructed with peculiar reference to abstract number as the subject of those operations. The Difference Engine is the embodying of one particular and very limited set of operations, which (see the notation used in Note B) may be expressed thus (+, +, +, +, +, +), or thus 6(+). Six repetitions of the one operation, +, is, in fact, the whole sum and object of that engine. It has seven columns, and a number on any column can add itself to a number on the next column to its right-hand. So that, beginning with the column furthest to the left, six additions can be effected, and the result appears on the seventh column, which is the last on the right-hand. The operating mechanism of this engine acts in as separate and independent a manner as that of the Analytical Engine; but being susceptible of only one unvarying and restricted combination, it has little force or interest in illustration of the distinct nature of the science of operations. The importance of regarding the Analytical Engine under this point of view will, we think, become more and more obvious as the reader proceeds with M. Menabrea's clear and mastery article. The calculus of operations is likewise in itself a topic of so much interest, and has of late years been so much more written on and thought on than formerly, that any bearing which that engine, from its mode of constitution, may possess upon the illustration of this branch of mathematical science should not be overlooked. Whether the inventor of this engine had any such views in his mind while working out the invention, or whether he may subsequently ever have regarded it under this phase, we do not know; but it is one that forcibly occurred to ourselves on becoming acquainted with the means through which analytical combinations are actually attained by the mechanism. We cannot forbear suggesting one practical result which it appears to us must be greatly facilitated by the independent manner in which the engine orders and combines its operations: we allude to the attainment of those combinations into which imaginary quantities enter. This is a branch of its processes into which we have not had the opportunity of inquiring, and our conjecture therefore as to the principle on which we conceive the accomplishment of such results may have been made to depend, is very probably not in accordance with the fact, and less subservient for the purpose than some other principles, or at least requiring the cooperation of others. It seems to us obvious, however, that where operations are so independent in their mode of acting, it must be easy, by means of a few simple provisions and additions in arranging the mechanism, to bring out a double set of results, viz. - 1st, the numerical magnitudes which are the results of operations performed on numerical data. (These results are the primary object of the engine.) 2ndly, the symbolical results to be attached to those numerical results, which symbolical results are not less the necessary and logical consequences of operations performed upon symbolical data, than are numerical results when the data are numerical[2].
If we compare together the powers and the principles of construction of the Difference and of the Analytical Engines, we shall perceive that the capabilities of the latter are immeasurably more extensive than those of the former, and that they in fact hold to each other the same relationship as that of analysis to arithmetic. The Difference Engine can effect but one particular series of operations, viz. that required for tabulating the integral of the special function
and as it can only do this for values of n up to 7[3], it cannot be considered as being the most general expression even of one particular function, much less as being the expression of any and all possible functions of all degrees of generality. The Difference Engine can in reality (as has been already partly explained) do nothing but add; and any other processes, not excepting those of simple subtraction, multiplication and division, can be performed by it only just to that extent in which it is possible, by judicious mathematical arrangement and artifices, to reduce them to a series of additions. The method of differences is, in fact, a method of additions; and as it includes within its means a larger number of results attainable by addition simply, than any other mathematical principle, it was very appropriately selected as the basis on which to construct an Adding Machine, so as to give to the powers of such a machine the widest possible range. The Analytical Engine, on the contrary, can either add, subtract, multiply or divide with equal facility; and performs each of these four operations in a direct manner, without the aid of any of the other three. This one fact implies everything; and it is scarcely necessary to point out, for instance, that while the Difference Engine can merely tabulate, and is incapable of developing, the Analytical Engine can either tabulate or develope.
The former engine is in its nature strictly arithmetical, and the results it can arrive at lie within a very clearly defined and restricted range, while there is no finite line of demarcation which limits the powers of the Analytical Engine. These powers are co-extensive with our knowledge of the laws of analysis itself, and need be bounded only by our acquaintance with the latter. Indeed we may consider the engine as the material and mechanical representative of analysis, and that our actual working powers in this department of human study will be enabled more effectually than heretofore to keep pace with our theoretical knowledge of its principles and laws, through the complete control which the engine gives us over the executive manipulation of algebraical and numerical symbols.
Those who view mathematical science, not merely as a vast body of abstract and immutable truths, whose intrinsic beauty, symmetry and logical completeness, when regarded in their connexion together as a whole, entitle them to a prominent place in the interest of all profound and logical minds, but as possessing a yet deeper interest for the human race, when it is remembered that this science constitutes the language through which alone we can adequately express the great facts of the natural world, and those unceasing changes of mutual relationship which, visibly or invisibly, consciously or unconsciously to our immediate physical perceptions, are interminably going on in the agencies of the creation we live amidst : those who thus think on mathematical truth as the instrument through which the weak mind of man can most effectually read his Creator's works, will regard with especial interest all that can tend to facilitate the translation of its principles into explicit practical forms.
The distinctive characteristic of the Analytical Engine, and that which has rendered it possible to endow mechanism with such extensive faculties as bid fair to make this engine the executive right-hand of abstract algebra, is the introduction into it of the principle which Jacquard devised for regulating, by means of punched cards, the most complicated patterns in the fabrication of brocaded stuffs. It is in this that the distinction between the two engines lies. Nothing of the sort exists in the Difference Engine. We may say most aptly, that the Analytical Engine weaves algebraical patterns just as the Jacquard-loom weaves flowers and leaves. Here, it seems to us, resides much more of originality than the Difference Engine can be fairly entitled to claim. We do not wish to deny to this later all such claims. We believe that it is the only proposal or attempt ever made to construct a calculating machine founded on the principle of successive orders of differences, and capable of printing off its own results; and that this engine surpasses its predecessors, both in the extent of the calculations which it can perform, in the facility, certainty and accuracy with which it can effect them, and in the absence of all necessity for the intervention of human intelligence during the performance of its calculations. Its nature is, however, limited to the strictly arithmetical, and it is far from being the first or only scheme for constructing arithmetical calculating machines with more or less of success.
The bounds of arithmetic were however outstepped the moment the idea of applying the cards had occurred; and the Analytical Engine does not occupy common ground with mere "calculating machines." It holds a position wholly its own; and the considerations it suggests are most interesting in their nature. In enabling mechanism to combine together general symbols in successions of unlimited variety and extent, a uniting link is established between the operations of matter and the abstract mental processes of the most abstract branch of mathematical science. A new, a vast, and a powerful language is developed for the future use of analysis, in which to wield its truths so that these may become of more speedy and accurate practical application for the purposes of mankind than the means hitherto in our possession have rendered possible. Thus not only the mental and the material, but the theoretical and the practical in the mathematical world, are brought into more intimate and effective connexion with each other. We are not aware of its being on record that anything partaking in the nature of what is so well designated the Analytical Engine has been hitherto proposed, or even thought of, as a practical possibility, any more than the idea of a thinking or of a reasoning machine.
We will touch on another point which constitutes an important distinction in the modes of operating of the Difference and Analytical Engines. In order to enable the former to do its business, it is necessary to put into its columns the series of numbers constituting the first terms of the several orders of differences for whatever is the particular table under consideration. The machine then works upon these as its data. But these data must themselves have been already computed through a series of calculations by a human head. Therefore that engine can only produce results depending on data which have been arrived at by the explicit and actual working out of processes that are in their nature different from any that come within the sphere of its own powers. In other words, an analysing process must have been gone through by a human mind in order to obtain the data upon which the engine then synthetically builds its results. The Difference Engine is in its character exclusively synthetical, while the Analytical Engine is equally capable of analysis or of synthesis.
It is true that the Difference Engine can calculate to a much greater extent with these few preliminary data, than the data themselves required for their own determination. The table of squares, for instance, can be calculated to any extent whatever, when the numbers one and two are furnished; and a very few differences computed at any part of a table of logarithms would enable the engine to calculate many hundreds or even thousands of logarithms. Still the circumstance of its requiring, as a previous condition, that any function whatever shall have been numerically worked out, makes it very inferior in its nature and advantages to an engine which, like the Analytical Engine, requires merely that we should know the succession and distribution of the operations to be performed; without there being any occasion[4], in order to obtain data on which it can work, for our ever having gone through either the same particular operations which it is itself to effect, or any others. Numerical data must of course be given it, but they are mere arbitrary ones; not data that could only be arrived at through a systematic and necessary series of previous numerical calculations, which is quite a different thing.
To this it may be replied, that an analysing process must equally have been performed in order to furnish the Analytical Engine with the necessary operative data; and that herein may also lie a possible source of error. Granted that the actual mechanism is unerring in its processes, the cards may give it wrong orders. This is unquestionably the case; but there is much less chance of error, and likewise far less expenditure of time and labour, where operations only, and the distribution of these operations, have to be made out, than where explicit numerical results are to be attained. In the case of the Analytical Engine we have undoubtedly to lay out a certain capital of analytical labour in one particular line; but this is in order that the engine may bring us in a much larger return in another line. It should be remembered also that the cards, when once made out for any formula, have all the generality of algebra, and include an infinite number of particular cases.
We have dwelt considerably on the distinctive peculiarities of each of these engines, because we think it essential to place their respective attributes in strong relief before the apprehension of the public; and to define with clearness and accuracy the wholly different nature of the principles on which each is based, so as to make it self-evident to the reader (the mathematical reader at least) in what manner and degree the powers of the Analytical Engine transcend those of an engine, which, like the Difference Engine, can only work out such results as may be derived from one restricted and particular series of processes, such as those included in Dnuz= 0. We think this of importance, because we know that there exists considerable vagueness and inaccuracy in the mind of persons in general on the subject. There is a misty notion amongst most of those who have attended at all to it, that two "calculating machines" have been successively invented by the same person within the last few years; while others again have never heard but of the one original "calculating machine," and are not aware of there being any extension upon this. For either of these two classes of persons the above considerations are appropriate. While the latter require a knowledge of the fact that there are two such inventions, the former are not less in want of accurate and well-defined information on the subject. No very clear or correct ideas prevail as to the characteristics of each engine, or their respective advantages or disadvantages; and in meeting with those incidental allusions, of a more or less direct kind, which occur in so many publications of the day, to these machines, it must frequently be matter of doubt which "calculating machine" is referred to, or whether both are included in the general allusion.
We are desirous likewise of removing two misapprehensions which we know obtain, to some extent, respecting these engines. In the first place it is very generally supposed that the Difference Engine, after it had been completed up to a certain point, suggested the idea of the Analytical Engine; and that the second is in fact the improved offspring of the first, and grew out of the existence of its predecessor, through some natural or else accidental combination of ideas suggested by this one. Such a supposition is in this instance contrary to the facts; although it seems to be almost an obvious inference, wherever two inventions, similar in their nature and objects, succeed each other closely in order of time, and strikingly in order of value; more especially when the same individual is the author of both. Nevertheless the ideas which led to the Analytical Engine occurred in a manner wholly independent of any that were connected with the Difference Engine. These ideas are indeed in their own intrinsic nature independent of the latter engine, and might equally have occurred had it never existed nor been even thought of at all.
The second of the misapprehensions above alluded to relates to the well-known suspension, during some years past, of all progress in the construction of the Difference Engine. Respecting the circumstances which have interfered with the actual completion of either invention, we offer no opinion; and in fact are not possessed of the data for doing so, had we the inclination. But we know that some persons suppose these obstacles (be they what they may) to have arisen in consequence of the subsequent invention of the Analytical Engine while the former was in progress. We have ourselves heard it even lamented that an idea should ever have occurred at all, which had turned out to be merely the means of arresting what was already in a course of successful execution, without substituting the superior invention in its stead. This notion we can contradict in the most unqualified manner. The progress of the Difference Engine had long been suspended, before there were even the least crude glimmerings of any invention superior to it. Such glimmerings, therefore, and their subsequent development, were in no way the original cause of that suspension; although, where difficulties of some kind or other evidently already existed, it was not perhaps calculated to remove or lessen them that an invention should have been meanwhile thought of, which, while including all that the first was capable of, possesses powers so extended as to eclipse it altogether.
We leave it for the decision of each individual (after he has possessed himself of competent information as to the characteristics of each engine) to determine how far it ought to be matter of regret that such an accession has been made to the powers of human science, even if it has (which we generally doubt) increased to a certain limited extent some already existing difficulties that had arisen in the way of completing a valuable but lesser work. We leave it for each to satisfy himself as to the wisdom of desiring the obliteration (were that now possible) of all records of the more perfect invention, in order that the comparatively limited one might be finished. The Difference Engine would doubtless fulfil all those practical objects which it was originally destined for. It would certainly calculate all the tables that are more directly necessary for the physical purposes of life, such as nautical and other computations. Those who incline to very strictly utilitarian views may perhaps feel that the peculiar powers of the Analytical Engine bear upon questions of abstract and speculative science, rather than upon those involving every-day and ordinary human interests. These persons being likely to possess but little sympathy, or possibly acquaintance, with any branches of science which they do not find to be useful (according to their definition of that word), may conceive that the undertaking of that engine, now that the other one is already in progress, would be a barren and unproductive laying out of yet more money and labour; in fact, a work of supererogation. Even in the utilitarian aspect, however, we do not doubt that very valuable practical results would be developed by the extended faculties of the Analytical Engine; some of which results we think we could now hint at, had we the space; and others, which it may not yet be possible to foresee, but which would be brought forth by the daily increasing requirements of science, and by a more intimate practical acquaintance with the powers of the engine, were it in actual existence.
On general grounds, both of an a priori description as well as those founded on the scientific history and experience of mankind, we see strong presumptions that such would be the case. Nevertheless all will probably concur in feeling that the completion of the Difference Engine would be far preferable to the non-completion of any calculating engine at all. With whomsoever or wheresoever may rest the present causes of difficulty that apparently exist towards either the completion of the old engine, or the commencement of the new one, we trust they will not ultimately result in this generation's being acquainted with these inventions through the medium of pen, ink and paper merely; and still more do we hope, that for the honour of our country's reputation in the future pages of history, these causes will not lead to the completion of the undertaking by some other nation or government. This could not but be matter of just regret; and equally so, whether the obstacles may have originated in private interests and feelings, in considerations of a more public description, or in causes combining the nature of both such solutions.
We refer the reader to the 'Edinburgh Review' of July 1834, for a very able account of the Difference Engine. The writer of the article we allude to has selected as his prominent matter for exposition, a wholly different view of the subject from that which M. Menabrea has chosen. The former chiefly treats it under its mechanical aspect, entering but slightly into the mathematical principles of which that engine is the representative, but giving, in considerable length, many details of the mechanism and contrivances by means of which it tabulates the various orders of differences. M. Menabrea, on the contrary, exclusively developes the analytical view; taking it for granted that mechanism is able to perform certain processes, but without attempting to explain how; and devoting his whole attention to explanations and illustrations of the manner in which analytical laws can be so arranged and combined as to bring every branch of that vast subject within the grasp of the assumed powers of mechanism. It is obvious that, in the invention of a calculating engine, these two branches of the subject are equally essential fields of investigation, and that on their mutual adjustment, one to the other, must depend all success. They must be made to meet each other, so that the weak points in the powers of either department may be compensated by the strong points in those of the other. They are indissolubly connected, though so different in their intrinsic nature, that perhaps the same mind might not be likely to prove equally profound or successful in both. We know those who doubt whether the powers of mechanism will in practice prove adequate in all respects to the demands made upon them in the working of such complicated trains of machinery as those of the above engines, and who apprehend that unforeseen practical difficulties and disturbances will arise in the way of accuracy and of facility of operation. The Difference Engine, however, appears to us to be in a great measure an answer to these doubts. It is complete as far as it goes, and it does work with all the anticipated success. The Analytical Engine, far from being more complicated, will in many respects be of simpler construction; and it is a remarkable circumstance attending it, that with very simplified means it is so much more powerful.
The article in the 'Edinburgh Review' was written some time previous to the occurrence of any ideas such as afterwards led to the invention of the Analytical Engine; and in the nature of the Difference Engine there is much less that would invite a writer to take exclusively, or even prominently, the mathematical view of it, than in that of the Analytical Engine; although mechanism has undoubtedly gone much further to meet mathematics, in the case of this engine, than of the former one. Some publication embracing the mechanical view of the Analytical Engine is a desideratum which we trust will be supplied before long.
Those who may have the patience to study a moderate quantity of rather dry details will find ample compensation, after perusing the article of 1834, in the clearness with which a succinct view will have been attained of the various practical steps through which mechanism can accomplish certain processes; and they will also find themselves still further capable of appreciating M. Menabrea's more comprehensive and generalized memoir. The very difference in the style and object of these two articles makes them peculiarly valuable to each other; at least for the purposes of those who really desire something more than a merely superficial and popular comprehension of the subject of calculating engines. A. A. L.
In the Difference Engine there are seven of these columns placed side by side in a row, and the working mechanism extends behind them: the general form of the whole mass of machinery is that of a quadrangular prism (more or less approaching to the cube); the results always appearing on that perpendicular face of the engine which contains the columns of discs, opposite to which face a spectator may place himself. In the Analytical Engine there would be many more of these columns, probably at least two hundred. The precise form and arrangement which the whole mass of its mechanism will assume is not yet finally determined.
We may conveniently represent the columns of discs on paper in a diagram like the following:-
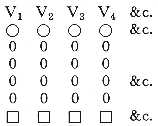
The V's are for the purpose of convenient reference to any column,
either in writing or speaking, and are consequently numbered. The reason
why the letter V is chosen for this purpose in preference to any other
letter, is because these columns are designated (as the reader will find
in proceeding with the Memoir) the Variables, and sometimes the
Variable columns, or the columns of Variables. The origin
of this appellation is, that the values on the columns are destined to
change, that is to vary, in every conceivable manner. But it is
necessary to guard against the natural misapprehension that the columns
are only intended to receive the values of the variables in an analytical
formula, and not of the constants. The columns are called Variables
on a ground wholly unconnected with the analytical distinction between
constants and variables. In order to prevent the possibility of confusion,
we have, both in the translation and in the notes, written Variable with
a capital letter when we use the word to signify a column of the engine,
and variable with a small letter when we mean the variable of a formula.
Similarly, Variable-cards signify any cards that belong to a column
of the engine.
To return to the explanation of the diagram: each circle at the top is intended to contain the algebraic sign + or -, either of which can be substituted[1] for the other, according as the number represented on the column below is positive or negative. In a similar manner any other purely symbolical results of algebraical processes might be made to appear in these circles. In Note A. the practicability of developing symbolical with no less ease than numerical results has been touched on. The zeros beneath the symbolic circles represent each of them a disc, supposed to have the digit 0 presented in front. Only four tiers of zeros have been figured in the diagram, but these may be considered as representing thirty or forty, or any number of tiers of discs that may be required. Since each disc can present any digit, and each circle any sign, the discs of every column may be so adjusted[2] as to express any positive or negative number whatever within the limits of the machine; which limits depend on the perpendicular extent of the mechanism, that is, on the number of discs to a column.
Each of the squares below the zeros is intended for the inscription of any general symbol or combination of symbols we please; it being understood that the number represented on the column immediately above is the numerical value of that symbol, or combination of symbols. Let us, for instance, represent the three quantities a, n, x, and let us further suppose that a = 5, n= 7, x = 98. We should have[3] -
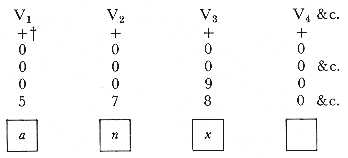
Let us select the first. It would stand as follows, previous to calculation:-
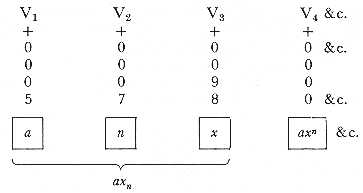
First, six multiplications in order to get xn (= 987
for the above particular data).
Secondly, one multiplication in order then to get a. xn
(= 5.987).
In all, seven multiplications to complete the whole process. We may thus represent them:-
The multiplications would, however, at successive stages in the solution of the problem, operate on pairs of numbers, derived from different columns. In other words, the same operation would be performed on different subjects of operation. And here again is an illustration of the remarks made in the preceding Note on the independent manner in which the engine directs its operations. In determining the value of axn, the operations are homogeneous, but are distributed amongst different subjects of operation, at successive stages of the computation. It is by means of certain punched cards, belonging to the Variables themselves, that the action of the operations is so distributed as to suit each particular function. The Operation-cards merely determine the succession of operations in a general manner. They in fact throw all that portion of the mechanism included in the mill into a series of different states, which we may call the adding state, or the multiplying state, &c. respectively. In each of these states the mechanism is ready to act in the way peculiar to that state, on any pair of numbers which may be permitted to come within its sphere of action. Only one of these operating states of the mill can exist at a time; and the nature of the mechanism is also such that only one pair of numbers can be received and acted on at a time. Now, in order to secure that the mill shall receive a constant supply of the proper pairs of numbers in succession, and that it shall also rightly locate the result of an operation performed upon any pair, each Variable has cards of its own belonging to it. It has, first, a class of cards whose business it is to allow the number on the Variable to pass into the mill, there to be operated upon. These cards may be called the Supplying-cards. They furnish the mill with its proper food. Each Variable has, secondly, another class of cards, whose office it is to allow the Variable to receive a number from the mill. These cards may be called the Receiving-cards. They regulate the location of results, whether temporary or ultimate results. The Variable-cards in general (including both the preceding classes) might, it appears to us, be even more appropriately designated the Distributive-cards, since it is through their means that the action of the operations, and the results of this action, are rightly distributed.
There are two varieties of the Supplying Variable-cards, respectively adapted for fulfilling two distinct subsidiary purposes: but as these modifications do not bear upon the present subject, we shall notice them in another place.
In the above case of axn, the Operation-cards merely order seven multiplications, that is, they order the mill to be in the multiplying state seven successive times (without any reference to the particular columns whose numbers are to be acted upon). The proper Distributive Variable-cards step in at each successive multiplication, and cause the distributions requisite for the particular case.
The engine might be made to calculate all these in succession. Having completed axn, the function xa n might be written under the brackets instead of axn, and a new calculation commenced (the appropriate Operation and Variable-cards for the new function of course coming into play). The results would then appear on V5. So on for any number of different functions of the quantities a, n, x. Each result might either permanently remain on its column during the succeeding calculations, so that when all the functions had been computed, their values would simultaneously exist on V4, V5, V6, &c.; or each result might (after being printed off, or used in any specified manner) be effaced, to make way for its successor. The square under V4 ought, for the latter arrangement, to have the functions axn, xa n, anx, &c. successively inscribed in it.
Let us now suppose that we have two expressions whose values have been computed by the engine independently of each other (each having its own group of columns for data and results). Let them be axn, and bpy. They would then stand as follows on the columns:-
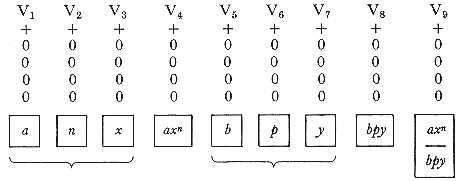
This example is introduced merely to show that we may, if we please, retain separately and permanently any intermediate results (like axn, bpy) which occur in the course of processes having an ulterior and more complicated result as their chief and final object (like ((axn) / (bpy)).
Any group of columns may be considered as representing a general function, until a special one has been implicitly impressed upon them through the introduction into the engine of the Operation and Variable-cards made out for a particular function. Thus, in the preceding example, V1, V2, V3, V5, V6, V7, represent the general function f(a, n, b, p, x, y) until the function (axn) / (bpy) has been determined on, and implicitly expressed by the placing of the right cards in the engine. The actual working of the mechanism, as regulated by these cards, then explicitly developes the value of the function. The inscription of a function under the brackets, and in the square under the result-column, in no way influences the processes or the results, and is merely a memorandum for the observer, to remind him of what is going on. It is the Operation and the Variable-cards only which in reality determine the function. Indeed it should be distinctly kept in mind, that the inscriptions within any of the squares are quite independent of the mechanism or workings of the engine, and are nothing but arbitrary memorandums placed there at pleasure to assist the spectator.
The further we analyse the manner in which such an engine performs its processes and attains its results, the more we perceive how distinctly it places in a true and just light the mutual relations and connexion of the various steps of mathematical analysis; how clearly it separates those things which are in reality distinct and independent, and unites those which are mutually dependent. A. A. L.
The mode of application of the cards, as hitherto used in the art of weaving, was not found, however, to be sufficiently powerful for all the simplifications which it was desirable to attain in such varied and complicated processes as those required in order to fulfil the purposes of an Analytical Engine. A method was devised of what was technically designated backing the cards in certain groups according to certain laws. The object of this extension is to secure the possibility of bringing any particular card or set of cards into use any number of times successively in the solution of one problem. Whether this power shall be taken advantage of or not, in each particular instance, will depend on the nature of the operations which the problem under consideration may require. The process is alluded to by M. Menabrea in page 16, and it is a very important simplification. It has been proposed to use it for the reciprocal benefit of that art, which, while it has itself no apparent connexion with the domains of abstract science, has yet proved so valuable to the latter, in suggesting the principles which, in their new and singular field of application, seem likely to place algebraical combinations not less completely within the province of mechanism, than are all those varied intricacies of which intersecting threads are susceptible. By the introduction of the system of backing into the Jacquard-loom itself, patterns which should possess symmetry, and follow regular laws of any extent, might be woven by means of comparatively few cards.
Those who understand the mechanism of this loom will perceive that the above improvement is easily effected in practice, by causing the prism over which the train of pattern-cards is suspended to revolve backwards instead of forwards, at pleasure, under the requisite circumstances; until, by so doing, any particular card, or set of cards, that has done duty once, and passed on in the ordinary regular succession, is brought back to the position it occupied just before it was used the preceding time. The prism then resumes its forward rotation, and thus brings the card or set of cards in question into play a second time. This process may obviously be repeated any number of times. A. A. L.
1st. Those on which the data are inscribed:
2ndly. Those intended to receive the final results:
3rdly. Those intended to receive such intermediate and temporary combinations of the primitive data as are not to be permanently retained, but are merely needed for working with, in order to attain the ultimate results. Combinations of this kind might properly be called secondary data. They are in fact so many successive stages towards the final result. The columns which receive them are rightly named Working-Variables, for their office is in its nature purely subsidiary to other purposes. They develope an intermediate and transient class of results, which unite the original data with the final results.
The Result-Variables sometimes partake of the nature of Working-Variables. It frequently happens that a Variable destined to receive a final result is the recipient of one or more intermediate values successively, in the course of the processes. Similarly, the Variables for data often become Working-Variables, or Result-Variables, or even both in succession. It so happens, however, that in the case of the present equations the three sets of offices remain throughout perfectly separate and independent.
It will be observed, that in the squares below the Working-Variables nothing is inscribed. Any one of these Variables is in many cases destined to pass through various values successively during the performance of a calculation (although in these particular equations no instance of this occurs). Consequently no one fixed symbol, or combination of symbols, should be considered as properly belonging to a merely Working-Variable; and as a general rule their squares are left blank. Of course in this, as in all other cases where we mention a general rule, it is understood that many particular exceptions may be expedient.
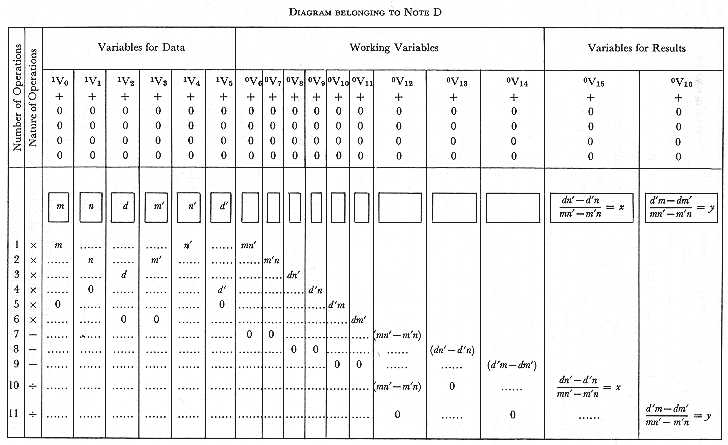
In order that all the indications contained in the diagram may be completely understood, we shall now explain two or three points, not hitherto touched on. When the value on any Variable is called into use, one of two consequences may be made to result. Either the value may return to the Variable after it has been used, in which case it is ready for a second use if needed; or the Variable may be made zero. (We are of course not considering a third case, of not unfrequent occurrence, in which the same Variable is destined to receive the result of the very operation which it has just supplied with a number.) Now the ordinary rule is, that the value returns to the Variable; unless it has been foreseen that no use for that value can recur, in which case zero is substituted. At the end of a calculation, therefore, every column ought as a general rule to be zero, excepting those for results. Thus it will be seen by the diagram, that when m, the value on V0, is used for the second time by Operation 5, V0 becomes 0, since m is not again needed; that similarly, when (mn' - m'n), on V12, is used for the third time by Operation 11, V12 becomes zero, since (mn' - m'n) is not again needed. In order to provide for the one or the other of the courses above indicated, there are two varieties of the Supplying Variable-cards. One of these varieties has provisions which cause the number given off from any Variable to return to that Variable after doing its duty in the mill. The other variety has provisions which cause zero to be substituted on the Variable, for the number given off. These two varieties are distinguished, when needful, by the respective appellations of the Retaining Supply-cards and the Zero Supply-cards. We see that the primary office (see Note B.) of both these varieties of cards is the same; they only differ in their secondary office.
Every Variable thus has belonging to it one class of Receiving Variable-cards and two classes of Supplying Variable-cards. It is plain however that only one or the other of these two latter classes can be used by any one Variable for one operation; never both simultaneously; their respective functions being mutually incompatible.
It should be understood that the Variable-cards are not placed in immediate contiguity with the columns. Each card is connected by means of wires with the column it is intended to act upon.
Our diagram ought in reality to be placed side by side with M. Menabrea's corresponding table, so as to be compared with it, line for line belonging to each operation. But is was unfortunately inconvenient to print them in this desirable form. The diagram is, in the main, merely another manner of indicating the various relations denoted in M. Menabrea's table. Each mode has some advantages and some disadvantages. Combined, they form a complete and accurate method of registering every step and sequence in all calculations performed by the engine.
No notice has yet been taken of the upper indices which are added to the left of each V in the diagram; an addition which we have also taken the liberty of making to the V's in M. Menabrea's tables of pages 14, 16, since it does not alter anything therein represented by him, but merely adds something to the previous indications of those tables. The lower indices are obviously indices of locality only, and are wholly independent of the operations performed or of the results obtained, their value continuing unchanged during the performance of calculations. The upper indices, however, are of a different nature. Their office is to indicate any alteration in the value which a Variable represents; and they are of course liable to changes during the processes of a calculation. Whenever a Variable has only zeros upon it, it is called 0V; the moment a value appears on it (whether that value be placed there arbitrarily, or appears in the natural course of a calculation), it becomes 1V. If this value gives place to another value, the Variable becomes 2V, and so forth. Whenever a value again gives place to zero, the Variable again becomes 0V, even if it have been nV the moment before. If a value then again be substituted, the Variable becomes n + 1 V (as it would have done if it had not passed through the intermediate 0V); &c. &c. Just before any calculation is commenced, and after the data have been given, and everything adjusted and prepared for setting the mechanism in action, the upper indices of the Variables for data are all unity, and those for the Working and Result-variables are all zero. In this state the diagram represents them[2].
There are several advantages in having a set of indices of this nature; but these advantages are perhaps hardly of a kind to be immediately perceived, unless by a mind somewhat accustomed to trace the successive steps by means of which the engine accomplishes its purposes. We have only space to mention in a general way, that the whole notation of the tables is made more consistent by these indices, for they are able to mark a difference in certain cases, where there would otherwise be an apparent identity confusing in its tendency. In such a case as Vn = Vp + Vn there is more clearness and more consistency with the usual laws of algebraical notation, in being able to write m + 1 Vn = qVp + mVn. It is also obvious that the indices furnish a powerful means of tracing back the derivation of any result; and of registering various circumstances concerning that series of successive substitutions, of which every result is in fact merely the final consequence; circumstances that may in certain cases involve relations which it is important to observe, either for purely analytical reasons, or for practically adapting the workings of the engine to their occurrence. The series of substitutions which lead to the equations of the diagram are as follow[3]:-
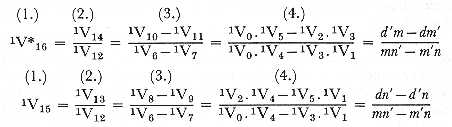
The substitutions in the preceding equations happen to be of little value towards illustrating the power and uses of the upper indices, for, owing to the nature of these particular equations, the indices are all unity throughout. We wish we had space to enter more fully into the relations which these indices would in many cases enable us to trace.
M. Menabrea incloses the three centre columns of his table under the general title Variable-cards. The V's however in reality all represent the actual Variable-columns of the engine, and not the cards that belong to them. Still the title is a very just one, since it is through the special action of certain Variable-cards (when combined with the more generalized agency of the Operation-cards) that every one of the particular relations he has indicated under that title is brought about.
Suppose we wish to ascertain how often any one quantity, or combination of quantities, is brought into use during a calculation. We easily ascertain this, from the inspection of any vertical column or columns of the diagram in which that quantity may appear. Thus, in the present case, we see that all the data, and all the intermediate results likewise, are used twice, excepting (mn' - m'n), which is used three times.
The order in which it is possible to perform the operations for the present example, enables us to effect all the eleven operations of which it consists with only three Operation cards; because the problem is of such a nature that it admits of each class of operations being performed in a group together; all the multiplications one after another, all the subtractions one after another, &c. The operations are {6 (x), 3 (-), 2 (÷)}.
Since the very definition of an operation implies that there must be two numbers to act upon, there are of course two Supplying Variable-cards necessarily brought into action for every operation, in order to furnish the two proper numbers. (See Note B.) Also, since every operation must produce a result, which must be placed somewhere, each operation entails the action of a Receiving Variable-card, to indicate the proper locality for the result. Therefore, at least three times as many Variable-cards as there are operations (not Operation-cards, for these, as we have just seen, are by no means always as numerous as the operations) are brought into use in every calculation. Indeed, under certain contingencies, a still larger population is requisite; such, for example, would probably be the case when the same result has to appear on more than one Variable simultaneously (which is not unfrequently a provision necessary for subsequent purposes in a calculation), and in some other cases which we shall not here specify. We see therefore that a great disproportion exists between the amount of Variable and of Operation-cards requisite for the working of even the simplest calculation.
All calculations do not admit, like this one, of the operations of the same nature being performed in groups together. Probably very few do so without exceptions occurring in one or other stage of the progress; and some would not admit it at all. The order in which the operations shall be performed in every particular case is a very interesting and curious question, on which our space does not permit us fully to enter. In almost every computation a great variety of arrangements for the succession of the processes is possible, and various considerations must influence the selection amongst them for the purposes of a Calculating Engine. One essential object is to choose that arrangement which shall tend to reduce to a minimum the time necessary for completing the calculation.
It must be evident how multifarious and how mutually complicated are the considerations which the workings of such an engine involve. There are frequently several distinct sets of effects going on simultaneously; all in a manner independent of each other, and yet to a greater or less degree exercising a mutual influence. To adjust each to every other, and indeed even to perceive and trace them out with perfect correctness and success, entails difficulties whose nature partakes to a certain extent of those involved in every question where conditions are very numerous and inter-complicated; such as for instance the estimation of the mutual relations amongst statistical phaenomena, and of those involved in many other classes of facts. A. A. L.
We have not subjoined any diagram of its development for this new example, as we did for the former one, because this is unnecessary after the full application already made of those diagrams to the illustration of M. Menabrea's excellent tables.
It may be remarked that a slight discrepancy exists between the formulae
given in the Memoir as the data for calculation, and the results of the calculation as developed in the last division of the table which accompanies it. To agree perfectly with this latter, the data should have been given as
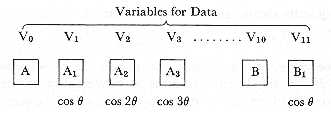
The following is a more complicated example of the manner in which the engine would compute a trigonometrical function containing variables. To multiply
by B + B1 cos q.
Let the resulting products be represented under the general form
This trigonometrical series is not only in itself very appropriate for illustrating the processes of the engine, but is likewise of much practical interest from its frequent use in astronomical computations. Before proceeding further with it, we shall point out that there are three very distinct classes of ways in which it may be desired to deduce numerical values from any analytical formula.
First. We may wish to find the collective numerical value of the whole formula, without any reference to the quantities of which that formula is a function, or to the particular mode of their combination and distribution, of which the formula is the result and representative. Values of this kind are of a strictly arithmetical nature in the most limited sense of the term, and retain no trace whatever of the processes through which they have been deduced. In fact, any one such numerical value may have been attained from an infinite variety of data, or of problems. The values for x and y in the two equations (see Note D.) come under this class of numerical results.
Secondly. We may propose to compute the collective numerical value of each term of a formula, or of a series, and to keep these results separate. The engine must in such a case appropriate as many columns to results as there are terms to compute.
Thirdly. It may be desired to compute the numerical value of various subdivisions of each term, and to keep all these results separate. It may be required, for instance, to compute each coefficient separately from its variable, in which particular case the engine must appropriate two result-columns to every term that contains both a variable and coefficient.
There are many ways in which it may be desired in special cases to distribute and keep separate the numerical values of different parts of an algebraical formula: and the power of effecting such distributions to any extent is essential to the algebraical character of the Analytical Engine. Many persons who are not conversant with mathematical studies, imagine that because the business of the engine is to give its results in numerical notation, the nature of its processes must consequently be arithmetical and numerical, rather than algebraical and analytical. This is an error. The engine can arrange and combine its numerical quantities exactly as if they were letters or any other general symbols; and in fact it might bring out its results in algebraical notation, were provisions made accordingly. It might develope three sets of results simultaneously, viz. symbolic results (as already alluded to in Notes A. and B.); numerical results (its chief and primary object); and algebraical results in literal notation. This latter however has not been deemed a necessary or desirable addition to its powers, partly because the necessary arrangements for effecting it would increase the complexity and extent of the mechanism to a degree that would not be commensurate with the advantages, where the main object of the invention is to translate into numerical language general formulae of analysis already known to us, or whose laws of formation are known to us. But it would be a mistake to suppose that because its results are given in the notation of a more restricted science, its processes are therefore restricted to those of that science. The object of the engine is in fact to give the utmost practical efficiency to the resources of numerical interpretations of the higher science of analysis, while it uses the processes and combinations of this latter.
To return to the trigonometrical series. We shall only consider the first four terms of the factor (A + A1 cos q + &c.), since this will be sufficient to show the method. We propose to obtain separately the numerical value of each coefficient Co, C1, &c. of (1.). The direct multiplication of the two factors gives
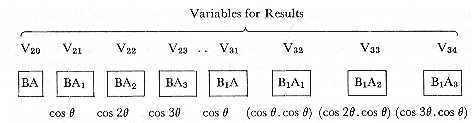
First Series of
Second Series of
Third Series, which con-
Operations.
Operations.
tains only one (final) operation.
1V10 x 1V0 = 1V20
1V11 x 1V0 = 1V31
1V21 + 1V31 = 2V21,
and
1V10 x 1V1 = 1V21
1V11 x 1V1 = 1V32
V31 becomes = 0.
1V10 x 1V2 = 1V22
1V11 x 1V2 = 1V33
1V10 x 1V3 = 1V23
1V11 x 1V3 = 1V34
We do not enter into the same detail of every step of the processes as in the examples of Notes D. and G., thinking it unnecessary and tedious to do so. The reader will remember the meaning and use of the upper and lower indices, &c., as before explained.
To proceed: we know that
Consequently, a slight examination of the second line of (2.) will show that by making the proper substitutions, (2.) will become
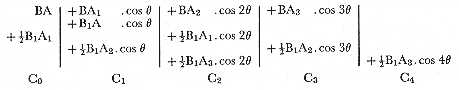
We shall perceive, if we inspect the particular arrangement of the results in (2.) on the Result-columns as represented in the diagram, that, in order to effect this transformation, each successive coefficient upon V32, V33, &c. (beginning with V32), must through means of proper cards be divided by two[2]; and that one of the halves thus obtained must be added to the coefficient on the Variable which precedes it by ten columns, and the other half to the coefficient on the Variable which precedes it by twelve columns; V32, V33, &c. themselves becoming zeros during the process.
This series of operations may be thus expressed[3]:-
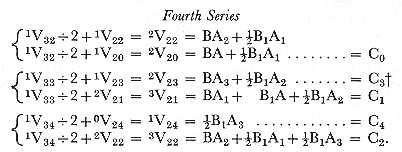
The substitution made by the engine of the processes in the second side of (3.) for those in the first side is an excellent illustration of the manner in which we may arbitrarily order it to substitute any function, number, or process, at pleasure, for any other function, number or process, on the occurrence of a specified contingency.
We will now suppose that we desire to go a step further, and to obtain the numerical value of each complete term of the product (1.); that is, of each coefficient and variable united, which for the (n + 1)th term would be Cn .cos n q.
We must for this purpose place the variables themselves on another set of columns, V41, V42, &c., and then order their successive multiplication by V21, V22, &c., each for each. There would thus be a final series of operations as follows:-
(N.B. that V40 being intended to receive the coefficient on V20 which has no variable, will only have cos 0 q (=1) inscribed on it, preparatory to commencing the fifth series of operations.)
From the moment that the fifth and final series of operations is ordered, the Variables V20, V21, &c. then in their turn cease to be Result-Variables and become mere Working-Variables; V40, V41, &c. being now the recipients of the ultimate results.
We should observe, that if the variables cos q, cos 2 q, cos 3 q, &c. are furnished, they would be placed directly upon V41, V42, &c., like any other data. If not, a separate computation might be entered upon in a separate part of the engine, in order to calculate them, and place them on V41, &c.
We have now explained how the engine might compute (1.) in the most direct manner, supposing we knew nothing about the general term of the resulting series. But the engine would in reality set to work very differently, whenever (as in this case) we do know the law for the general term.
The first two terms of (1.) are
and the general term for all these is
which is the coefficient of the (n + 1)th term. The engine would calculate the first two terms by means of a separate set of suitable Operation-cards, and would then need another set for the third term; which last set of Operation-cards would calculate all the succeeding terms ad infinitum, merely requiring certain new Variable-cards for each term to direct the operations to act on the proper columns. The following would be the successive sets of operations for computing the coefficients of n + 2 terms:-
Or we might represent them as follows, according to the numerical order of the operations:-
The brackets, it should be understood, point out the relation in which the operations may be grouped, while the comma marks succession. The symbol + might be used for this latter purpose, but this would be liable to produce confusion, as + is also necessarily used to represent one class of the actual operations which are the subject of that succession. In accordance with this meaning attached to the comma, care must be taken when any one group of operations recurs more than once, as is represented above by n (11 . . .15), not to insert a comma after the number or letter prefixed to that group. n, (11 . . . 15) would stand for an operation n, followed by the group of operations (11 . . . 15); instead of denoting the number of groups which are to follow each other.
Wherever a general term exists, there will be a recurring group of operations, as in the above example. Both for brevity and for distinctness, a recurring group is called a cycle. A cycle of operations, then, must be understood to signify any set of operations which is repeated more than once. It is equally a cycle, whether it be repeated twice only, or an infinite number of times; for it is the fact of a repetition occurring at all that constitutes it such. In many cases of analysis there is a recurring group of one or more cycles; that is, a cycle of a cycle, or a cycle of cycles. For instance: suppose we wish to divide a series by a series,
(1.)
a + bx + cx2+ . .
. . . ,
a' + b'x + c'x2 + . . . .
.
it being required that the result shall be developed, like the dividend
and the divisor, in successive powers of x. A little consideration
of (1.), and of the steps through which algebraical division is effected,
will show that (if the denominator be supposed to consist of p terms)
the first partial quotient will be completed by the following operations:-
(2.) { (÷ ), p (x, -)} or {(1), p (2, 3)},
that the second partial quotient will be completed by an exactly similar set of operations, which acts on the remainder obtained by the first set, instead of on the original dividend. The whole of the processes therefore that have been gone through, by the time the second partial quotient has been obtained, will be,-
(3.) 2{(÷ ), p (x, -)} or 2{(1), p (2, 3)},
which is a cycle that includes a cycle, or a cycle of the second order. The operations for the complete division, supposing we propose to obtain n terms of the series constituting the quotient, will be,-
(4.) n {(÷ ), p (x, -)} or n {(1), p (2, 3)}.
It is of course to be remembered that the process of algebraical division in reality continues ad infinitum, except in the few exceptional cases which admit of an exact quotient being obtained. The number n in the formula (4.) is always that of the number of terms we propose to ourselves to obtain; and the nth partial quotient is the coefficient of the (n - 1)th power of x.
There are some cases which entail cycles of cycles of cycles, to an indefinite extent. Such cases are usually very complicated, and they are of extreme interest when considered with reference to the engine. The algebraical development in a series of the nth function of any given function is of this nature. Let it be proposed to obtain the nth function of
(5.) f(a, b, c . . . . . . x), x being the variable.
We should premise, that we suppose the reader to understand what is meant by an nth function. We suppose him likewise to comprehend distinctly the difference between developing an nth function algebraically, and merely calculating an nth function arithmetically. If he does not, the following will be by no means very intelligible; but we have not space to give any preliminary explanations. To proceed: the law, according to which the successive functions of (5.) are to be developed, must of course first be fixed on. This law may be of very various kinds. We may propose to obtain our results in successive powers of x, in which case the general form would be
or in successive powers of n itself, the index of the function we are ultimately to obtain, in which case the general form would be
and x would only enter in the coefficients. Again, other functions of x or of n instead of powers might be selected. It might be in addition proposed, that the coefficients themselves should be arranged according to given functions of a certain quantity. Another mode would be to make equations arbitrarily amongst the coefficients only, in which case the several functions, according to either of which it might be possible to develope the nth function of (5.), would have to be determined from the combined consideration of these equations and of (5.) itself.
The algebraical nature of the engine (so strongly insisted on in a previous part of this Note) would enable it to follow out any of these various modes indifferently; just as we recently showed that it can distribute and separate the numerical results of any one prescribed series of processes, in a perfectly arbitrary manner. Were it otherwise, the engine could merely compute the arithmetical nth function, a result which, like any other purely arithmetical results, would be simply a collective number, bearing no traces of the data or the processes which had led to it.
Secondly, the law of development for the nth function being selected, the next step would obviously be to develope (5.) itself, according to this law. This result would be the first function, and would be obtained by a determinate series of processes. These in most cases would include amongst them one or more cycles of operations.
The third step (which would consist of the various processes necessary for effecting the actual substitution of the series constituting the first function, for the variable itself) might proceed in either of two ways. It might make the substitution either wherever x occurs in the original (5.), or it might similarly make it wherever x occurs in the first function itself which is the equivalent of (5.). In some cases the former mode might be best, and in others the latter.
Whichever is adopted, it must be understood that the result is to appear arranged in a series following the law originally prescribed for the development of the nth function. This result constitutes the second function; with which we are to proceed exactly as we did with the first function, in order to obtain the third function, and so on, n - 1 times, to obtain the nth function. We easily perceive that since every successive function is arranged in a series following the same law, there would (after the first function is obtained) be a cycle of a cycle, &c. of operations[6], one, two, three, up to n - 1 times, in order to get the nth function. We say, after the first function is obtained, because (for reasons on which we cannot here enter) the first function might in many cases be developed through a set of processes peculiar to itself, and not recurring for the remaining functions.
We have given but a very slight sketch of the principal general steps which would be requisite for obtaining an nth function of such a formula as (5.). The question is so exceedingly complicated, that perhaps few persons can be expected to follow, to their own satisfaction, so brief and general a statement as we are here restricted to on this subject. Still it is a very important case as regards the engine, and suggests ideas peculiar to itself, which we should regret to pass wholly without allusion. Nothing could be more interesting than to follow out, in every detail, the solution by the engine of such a case as the above; but the time, space and labour this would necessitate, could only suit a very extensive work.
To return to the subject of cycles of operations: some of the notation of the integral calculus lends itself very aptly to express them: (2.) might be thus written:-
(6.) (÷), S( + 1 )p ( x, - ) or (1), S( + 1 )p (2, 3),
where p stands for the variable; ( + 1 )p for the function of the variable, that is, for f p; and the limits are from 1 to p, or from 0 to p - 1, each increment being equal to unity. Similarly, (4.) would be, -
(7.) S( + 1 )n {(÷), S( + 1 )p ( x, - )}
the limits of n being from 1 to n, or from 0 to n - 1,
(8.) or S( + 1 )n { (1), S( + 1 )p (2, 3)}.
Perhaps it may be thought that this notation is merely a circuitous way of expressing what was more simply and effectually expressed before; and, in the above example, there may be some truth in this. But there is another description of cycles which can only effectually be expressed, in a condensed form, by the preceding notation. We shall call them varying cycles. They are of frequent occurrence, and include successive cycles of operations of the following nature:-
(9.) p (1, 2, . . m), (p - 1) (1, 2, . . . m), (p - 2) (1, 2, . . m) . . . (p - n) (1, 2 . . m), [7]
where each cycle contains the same group of operations, but in which the number of repetitions of the group varies according to a fixed rate, with every cycle. (9.) can be well expressed as follows:-
(10.) S p (1, 2, . . m), the limits of p being from p - n to p.
Independent of the intrinsic advantages which we thus perceive to result in certain cases from this use of the notation of the integral calculus, there are likewise considerations which make it interesting, from the connections and relations involved in this new application. It has been observed in some of the former Notes, that the processes used in analysis form a logical system of much higher generality than the applications to number merely. Thus, when we read over any algebraical formula, considering it exclusively with reference to the processes of the engine, and putting aside for the moment its abstract signification as to the relations of quantity, the symbols +, x, &c. in reality represent (as their immediate and proximate effect, when the formula is applied to the engine) that a certain prism which is a part of the mechanism (see Note C.) turns a new face, and thus presents a new card to act on the bundles of levers of the engine; the new card being perforated with holes, which are arranged according to the peculiarities of the operation of addition, or of multiplication, &c. Again, the numbers in the preceding formula (8.), each of them really represents one of these very pieces of card that are hung over the prism.
Now in the use made in the formulae (7.), (8.) and (10.), of the notation
of the integral calculus, we have glimpses of a similar new application
of the language of the higher mathematics. S,
in reality, here indicates that when a certain number of cards have acted
in succession, the prism over which they revolve must rotate backwards,
so as to bring those cards into their former position; and the limits 1
to n, 1 to p, &c., regulate how often this backward rotation
is to be repeated.
A. A. L.
The power of repeating the cards, alluded to by M. Menabrea in page 16, and more fully explained in Note C., reduces to an immense extent the number of cards required. It is obvious that this mechanical improvement is especially applicable wherever cycles occur in the mathematical operations, and that, in preparing data for calculations by the engine, it is desirable to arrange the order and combination of the processes with a view to obtain them as much as possible symmetrically and in cycles, in order that the mechanical advantages of the backing system may be applied to the utmost. It is here interesting to observe the manner in which the value of an analytical resourse is met and enhanced by an ingenious mechanical contrivance. We see in it an instance of one of those mutual adjustments between the purely mathematical and the mechanical departments, mentioned in Note A. as being a main and essential condition of success in the invention of a calculating engine. The nature of the resources afforded by such adjustments would be of two principal kinds. In some cases, a difficulty (perhaps in itself insurmountable) in the one department would be overcome by facilities in the other; and sometimes (as in the present case) a strong point in the one would be rendered still stronger and more available by combination with a corresponding strong point in the other.
As a mere example of the degree to which the combined systems of cycles and of backing can diminish the number of cards requisite, we shall choose a case which places it in strong evidence, and which has likewise the advantage of being a perfectly different kind of problem from those that are mentioned in any of the other Notes. Suppose it be required to eliminate nine variables from ten simple equations of the form -
We should explain, before proceeding, that it is not our object to consider this problem with reference to the actual arrangement of the data on the Variables of the engine, but simply as an abstract question of the nature and number of the operations required to be performed during its complete solution.
The first step would be the elimination of the first unknown quantity
x0 between the first two equations.
This would be obtained by the form -
for which the operations 10 (x, x, -) would be needed. The second step would be the elimination of x0 between the second and third equations, for which the operations would be precisely the same. We should then have had altogether the following operations:-
Continuing in the same manner, the total number of operations for the complete elimination of x0 between all the successive pairs of equations would be -
We should then be left with nine simple equations of nine variables from which to eliminate the next variable x1, for which the total of the processes would be -
We should then be left with eight simple equations of eight variables from which to eliminate x2, for which the processes would be -
and so on. The total operations for the elimination of all the variables would thus be -
So that three Operation-cards would perform the office of 330 such cards.
If we take n simple equations containing n - 1 variables, n being a number unlimited in magnitude, the case becomes still more obvious, as the same three cards might then take the place of thousands or millions of cards.
We shall now draw further attention to the fact, already noticed, of its being by no means necessary that a formula proposed for solution should ever have been actually worked out, as a condition for enabling the engine to solve it. Provided we know the series of operations to be gone through, that is sufficient. In the foregoing instance this will be obvious enough on a slight consideration. And it is a circumstance which deserves particular notice, since herein may reside a latent value of such an engine almost incalculable in its possible ultimate results. We already know that there are functions whose numerical value it is of importance for the purposes both of abstract and of practical science to ascertain, but whose determination requires processes so lengthy and so complicated, that, although it is possible to arrive at them through great expenditure of time, labour and money, it is yet on these accounts practically almost unattainable; and we can conceive there being some results which it may be absolutely impossible in practice to attain with any accuracy, and whose precise determination it may prove highly important for some of the future wants of science, in its manifold, complicated and rapidly-developing fields of inquiry, to arrive at.
Without, however, stepping into the region of conjecture, we will mention a particular problem which occurs to us at this moment as being an apt illustration of the use to which such an engine may be turned for determining that which human brains find it difficult or impossible to work out unerringly. In the solution of the famous problem of the Three Bodies, there are, out of about 295 coefficients of lunar perturbations given by M. Clausen (Astroe. Nachrichten, No. 406) as the result of the calculations by Burg, of two by Damoiseau, and of one by Burckhardt, fourteen coefficients that differ in the nature of their algebraic sign; and out of the remainder there are only 101 (or about one-third) that agree precisely both in signs and in amount. These discordances, which are generally small in individual magnitude, may arise either from an erroneous determination of the abstract coefficients in the development of the problem, or from discrepancies in the data deduced from observation, or from both causes combined. The former is the most ordinary source of error in astronomical computations, and this the engine would entirely obviate.
We might even invent laws for series or formulae in an arbitrary manner, and set the engine to work upon them, and thus deduce numerical results which we might not otherwise have thought of obtaining; but this would hardly perhaps in any instance be productive of any great practical utility, or calculated to rank higher than as a kind of philosophical amusement. A. A. L.
The Analytical Engine has no pretensions whatever to originate anything. It can do whatever we know how to order it to perform. It can follow analysis; but it has no power of anticipating any analytical relations or truths. Its province is to assist us in making available what we are already acquainted with. This it is calculated to effect primarily and chiefly of course, through its executive faculties; but it is likely to exert an indirect and reciprocal influence on science itself in another manner. For, in so distributing and combining the truths and the formulae of analysis, that they may become most easily and rapidly amenable to the mechanical combinations of the engine, the relations and the nature of many subjects in that science are necessarily thrown into new lights, and more profoundly investigated. This is a decidedly indirect, and a somewhat speculative, consequence of such an invention. It is however pretty evident, on general principles, that in devising for mathematical truths a new form in which to record and throw themselves out for actual use, views are likely to be induced, which should again react on the more theoretical phase of the subject. There are in all extensions of human power, or additions to human knowledge, various collateral influences, besides the main and primary object attained.
To return to the executive faculties of this engine: the question must arise in every mind, are they really even able to follow analysis in its whole extent? No reply, entirely satisfactory to all minds, can be given to this query, excepting the actual existence of the engine, and actual experience of its practical results. We will however sum up for each reader's consideration the chief elements with which the engine works:-
1. It performs the four operations of simple arithmetic upon any numbers whatever.
2. By means of certain artifices and arrangements (upon which we cannot enter within the restricted space which such a publication as the present may admit of), there is no limit either to the magnitude of the numbers used, or to the number of quantities (either variables or constants) that may be employed.
3. It can combine these numbers and these quantities either algebraically or arithmetically, in relations unlimited as to variety, extent, or complexity.
4. It uses algebraic signs according to their proper laws, and developes the logical consequences of these laws.
5. It can arbitrarily substitute any formula for any other; effacing the first from the columns on which it is represented, and making the second appear in its stead.
6. It can provide for singular values. Its power of doing this is referred to in M. Menabrea's memoir, page 17, where he mentions the passage of values through zero and infinity. The practicability of causing it arbitrarily to change its processes at any moment, on the occurrence of any specified contingency (of which its substitution of (1/2 cos .(n + 1) q + 1/2 cos .(n - 1) q)[1] for (cos .n q .cos .q), explained in Note E., is in some degree an illustration), at once secures this point.
The subject of integration and of differentiation demands some notice. The engine can effect these processes in either of two ways:-
First. We may order it, by means of the Operation and of the Variable-cards, to go through the various steps by which the required limit can be worked out for whatever function is under consideration.
Secondly. It may (if we know the form of the limit for the function in question) effect the integration or differentiation by direct[2] substitution. We remarked in Note B., that any set of columns on which numbers are inscribed, represents merely a general function of the several quantities, until the special function have been impressed by means of the Operation and Variable-cards. Consequently, if instead of requiring the value of the function, we require that of its integral, or of its differential coefficient, we have merely to order whatever particular combination of the ingredient quantities may constitute that integral or that coefficient. In axn, for instance, instead of the quantities
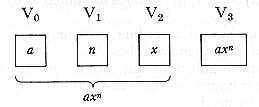
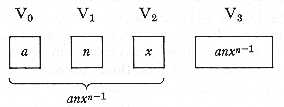
An interesting example for following out the processes of the engine would be such a form as
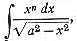
The methods in Arbogast's Calcul des Dérivations are peculiarly fitted for the notation and the processes of the engine. Likewise the whole of the Combinatorial Analysis, which consists first in a purely numerical calculation of indices, and secondly in the distribution and combination of the quantities according to laws prescribed by these indices.
We will terminate these Notes by following up in detail the steps through which the engine could compute the Numbers of Bernoulli, this being (in the form in which we shall deduce it) a rather complicated example of its powers. The simplest manner of computing these numbers would be from the direct expansion of
which is in fact a particular case of the development of
mentioned in Note E. Or again, we might compute them from the well-known form
or from the form
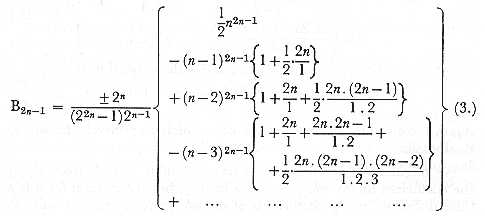
(in which B1, B3 . . . ., &c. are the Numbers of Bernoulli), we expand the denominator of the first side in powers of x, and then divide both numerator and denominator by x, we shall derive
If this latter multiplication be actually performed, we shall have a series of the general form
in which we see, first, that all the coefficients of the powers of x are severally equal to zero; and secondly, that the general form for D2n, the coefficient of the 2n + 1th term (that is of x2n any even power of x), is the following:-
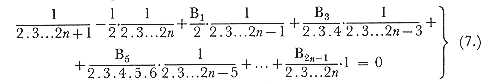
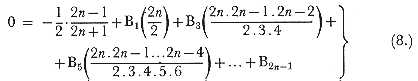
We might have derived a form nearly similar to (8.), from D2n -1the coefficient of any odd power of x in (6.); but the general form is a little different for the coefficients of the odd powers, and not quite so convenient.
On examining (7. ) and (8.), we perceive that, when these formulae are isolated from (6.), whence they are derived, and considered in themselves separately and independently, n may be any whole number whatever; although when (7.) occurs as one of the D's in (6.), it is obvious that n is then not arbitrary, but is always a certain function of the distance of that D from the beginning. If that distance be = d, then
It is with the independent formula (8.) that we have to do. Therefore
it must be remembered that the conditions for the value of n are
now modified, and that n is a perfectly arbitrary whole number.
This circumstance, combined with the fact (which we may easily perceive)
that whatever n is, every term of (8.) after the (n + 1)th
is = 0, and that the (n + 1)th term itself is always = B2n
- 1. 1/1 = B2n - 1, enables us to find
the value (either numerical or algebraical) of any nth Number of
Bernoulli B2n -1, in terms of all the preceding
ones, if we but know the values of B1, B3 . .
. . B2 n -3. We append to this Note a Diagram and Table,
containing the details of the computation for B7, (B1,
B3, B5 being supposed given).
On attentively considering (8.), we shall likewise perceive that we may derive from it the numerical value of every Number of Bernoulli in succession, from the very beginning, ad infinitum, by the following series of computations:-
1st Series. - Let n = 1, and calculate (8.) for this value of n. The result is B1.
2nd Series.- Let n = 2. Calculate (8.) for this value of n, substituting the value of B1 just obtained. The result is B3.
3rd Series. - Let n = 3. Calculate (8.) for this value of n,
substituting the values of B1, B3 before obtained.
The result is B5. And so on, to any extent.
The diagram[3] represents the columns of the engine when just prepared for computing B2n - 1 (in the case of n = 4); while the table beneath them presents a complete simultaneous view of all the successive changes which these columns then severally pass through in order to perform the computation. (The reader is referred to Note D. for explanations respecting the nature and notation of such tables.)
Six numerical data are in this case necessary for making the
requisite combinations. These data are 1, 2, n(=4), B1,
B3, B5. Were n = 5, the additional datum B7
would be needed. Were n = 6, the datum B9 would be needed;
and so on. Thus the actual number of data needed will always be
n + 2, for n = n; and out of these n + 2 data,
((n + 2) - 3)[4]
of them are successive Numbers of Bernoulli. The reason why the Bernoulli
Numbers used as data are nevertheless placed on Result-columns in
the diagram, is because they may properly be supposed to have been previously
computed in a succession by the engine itself; under which circumstances
each B will appear as a result, previous to being used as a datum
for computing the succeeding B. Here then is an instance (of the kind alluded
to in Note D.) of the same Variables filling more than
one office in turn. It is true that if we consider our computation of B7
as a perfectly isolated calculation, we may conclude B1,
B3, B5 to have been arbitrarily placed on the columns;
and it would then perhaps be more consistent to put them on V4,
V5, V6 as data and not results. But we are not taking
this view. On the contrary, we suppose the engine to be in the course
of computing the Numbers to an indefinite extent, from the very beginning;
and that we merely single out, by way of example, one amongst the
successive but distinct series' of computations it is thus performing.
Where the B's are fractional, it must be understood that they are computed
and appear in the notation of decimal fractions. Indeed this is
a circumstance that should be noticed with reference to all calculations.
In any of the examples already given in the translation and in the Notes,
some of the data, or of the temporary or permanent results, might
be fractional, quite as probably as whole numbers. But the arrangements
are so made, that the nature of the processes would be the same as for
whole numbers.
In the above table and diagram we are not considering the signs of any of the B's, merely their numerical magnitude. The engine would bring out the sign for each of them correctly of course, but we cannot enter on every additional detail of this kind as we might wish to do. The circles for the signs are therefore intentionally left blank in the diagram.
Operation-cards 1, 2, 3, 4, 5, 6, prepare - 1 .
2 n - 1. Thus, Card 1 multiplies two into n,
and the three
2 2 n + 1
Receiving Variable-cards belonging respectively to V4,
V5, V6, allow the result 2n to be placed on
each of these latter columns (this being a case in which a triple receipt
of the result is needed for subsequent purposes);
we see that the upper indices of the two Variables used, during Operation
1, remain unaltered.
We shall not go through the details of every operation singly, since the table and diagram sufficiently indicate them; we shall merely notice some few peculiar cases.
By Operation 6, a positive quantity is turned into a negative quantity, by simply subtracting the quantity from a column which has only zero upon it. (The sign at the top of V8 would become - during this process.)
Operation 7 will be unintelligible, unless it be remembered that if we were calculating for n = 1 instead of n = 4, Operation 6 would have completed the computation of B1 itself; in which case the engine, instead of continuing its processes, would have to put B1 on V21 ; and then either to stop altogether, or to begin Operations 1, 2 . . . . 7 all over again for value of n (=2), in order to enter on the computation of B3; (having however taken care, previous to this recommencement, to make the number on V3 equal to two, by the addition of unity to the former n = 1 on that column). Now Operation 7 must either bring out a result equal to zero (if n = 1); or a result greater than zero, as in the present case; and the engine follows the one or the other of the two courses just explained, contingently on the one or the other result of Operation 7. In order fully to perceive the necessity of this experimental operation, it is important to keep in mind what was pointed out, that we are not treating a perfectly isolated and independent computation, but one of a series of antecedent and prospective computations.
Cards 8, 9, 10 produce - 1 . 2 n - 1 + B1
2 n . In Operation 9 we see an
example of an upper index
2 2 n + 1
2
which again becomes a value after having passed from preceding values
to zero. V11 has successively been 0V11,
1V11, 2V11, 0V11,
3V11; and, from the nature of the office which V11
performs in the calculation, its index will continue to go through further
changes of the same description, which, if examined, will be found to be
regular and periodic.
Card 12 has to perform the same office as Card 7 did in the preceding section; since, if n had been = 2, the 11th operation would have completed the computation of B3.
Cards 13 to 20 make A3. Since A2 n -1 always consists of 2 n - 1 factors, A3 has three factors; and it will be seen that Cards 13, 14, 15, 16 make the second of these factors, and then multiply it with the first; and that 17, 18, 19, 20 make the third factor, and then multiply this with the product of the two former factors.
Card 23 has the office of Cards 11 and 7 to perform, since if n were = 3, the 21st and 22nd operations would complete the computation of B5. As our case is B7, the computation will continue one more stage; and we must now direct attention to the fact, that in order to compute A7, it is merely necessary precisely to repeat the group of Operations 13 to 20; and then, in order to complete the computation of B7, to repeat Operations 21, 22.
It will be perceived that every unit added to n in B2 n - 1, entails an additional repetition of operations (13 . . . 23) for the computation of B2 n -1. Not only are all the operations precisely the same however for every such repetition, but they require to be respectively supplied with numbers from the very same pairs of columns; with only the one exception of Operation 21, which will of course need B5 (from V23) instead of B3 (from V22). This identity in the columns which supply the requisite numbers must not be confounded with identity in the values those columns have upon them and give out to the mill. Most of those values undergo alterations during a performance of the operations (13 . . . 23), and consequently the columns present a new set of values for the next performance of (13 . . . 23) to work on.
At the termination of the repetition of operations (13 . . .
23) in computing B7, the alterations in the values on the Variables
are, that
V6 = 2n - 4 instead of 2n -2.
V7 = 6 . . . . . . . . . . . 4.
V10 = 0 . . . . . . . . . . 1.
V13 = A0 + A1 B1 + A3
B3 + A5 B5 instead of A0
+ A1 B1 + A3 B3.
In this state the only remaining processes are, first, to transfer the value which is on V13 to V24; and secondly, to reduce V6, V7, V13 to zero, and to add[5] one to V3, in order that the engine may be ready to commence computing B9. Operations 24 and 25 accomplish these purposes. It may be thought anomalous that Operation 25 is represented as leaving the upper index of V3 still = unity; but it must be remembered that these indices always begin anew for a separate calculation, and that Operation 25 places upon V3 the first value for the new calculation.
It should be remarked, that when the group (13 . . . 23) is repeated, changes occur in some of the upper indices during the course of the repetition: for example, 3V6 would become 4V6 and 5V6.
We thus see that when n = 1, nine Operation-cards are used; that
when n = 2, fourteen Operation-cards are used; and that when n
> 2, twenty-five Operation-cards are used; but that no more are
needed, however great n may be; and not only this, but that these
same twenty-five cards suffice for the successive computation of all the
Numbers from B1 to
B2 n - 1 inclusive. With respect to the number of
Variable-cards, it will be remembered, from the explanations in
previous Notes, that an average of three such cards to each operation
(not however to each Operation-card) is the estimate. According
to this, the computation of B1 will require twenty-seven Variable-cards;
B3 forty-two such cards; B5 seventy-five; and for
every succeeding B after B5, there would be thirty-three additional
Variable-cards (since each repetition of the group (13 . . . 23) adds eleven
to the number of operations required for computing the previous B). But
we must now explain, that whenever there is a cycle of operations,
and if these merely require to be supplied with numbers from the same
pairs of columns, and likewise each operation to place its result
on the same column for every repetition of the whole group,
the process then admits of a cycle of Variable-cards for effecting
its purposes. There is obviously much more symmetry and simplicity in the
arrangements, when cases do admit of repeating the Variable as well as
the Operation-cards. Our present example is of this nature. The only exception
to a perfect identity in all the processes and columns used,
for every repetition of Operations (13 . . . 23), is, that Operation 21
always requires one of its factors from a new column, and Operation 24
always puts its result on a new column. But as these variations follow
the same law at each repetition (Operation 21 always requiring its factor
from a column one in advance of that which it used the previous
time, and Operation 24 always putting its result on the column one in
advance of that which received the previous result), they are easily provided
for in arranging the recurring group (or cycle) of Variable-cards.
We may here remark, that the average estimate of three Variable-cards coming into use to each operation, is not to be taken as an absolutely and literally correct amount for all cases and circumstances. Many special circumstances, either in the nature of a problem, or in the arrangements of the engine under certain contingencies, influence and modify this average to a greater or less extent; but it is a very safe and correct general rule to go upon. In the preceding case it will give us seventy-five Variable-cards as the total number which will be necessary for computing any B after B3. This is very nearly the precise amount really used, but we cannot here enter into the minutiae of the few particular circumstances which occur in this example (as indeed at some one stage or other of probably most computations) to modify slightly this number.
It will be obvious that the very same seventy-five Variable-cards may be repeated for the computation of every succeeding Number, just on the same principle as admits of the repetition of the thirty-three Variable-cards of Operations (13 . . . 23) in the computation of any one Number. Thus there will be a cycle of a cycle of Variable-cards.
If we now apply the notation for cycles, as explained in Note E., we may express the operations for computing the Numbers of Bernoulli in the following manner:-
Again,
represents the total operations for computing every number in succession, from B1 to B2 n - 1 inclusive.
In this formula we see a varying cycle of the first order, and an ordinary cycle of the second order. The latter cycle in this case includes in it the varying cycle.
On inspecting the ten Working-Variables of the diagram, it will be perceived, that although the value on any one of them (excepting V4 and V5) goes through a series of changes, the office which each performs is in this calculation fixed and invariable. Thus V6 always prepares the numerators of the factors of any A; V7 the denominators. V8 always receives the (2n - 3)th factor of A2n - 1 , and V9 the (2 n - 1)th. V10 always decides which of two courses the succeeding processes are to follow, by feeling for the value of n through means of a subtraction; and so on; but we shall not enumerate further. It is desirable in all calculations so to arrange the processes, that the offices performed by the Variables may be as uniform and fixed as possible.
Supposing that it was desired not only to tabulate B1, B3, &c., but A0, A1, &c.; we have only then to appoint another series of Variables, V41, V42, &c., for receiving these latter results as they are successively produced upon V11. Or again, we may, instead of this, or in addition to this second series of results, wish to tabulate the value of each successive total term of the series (8.), viz. A0, A1 B1, A3 B3, &c. We have then merely to multiply each B with each corresponding A, as produced, and to place these successive products on Result-columns appointed for the purpose.
The formula (8.) is interesting in another point of view. It is one particular case of the general Integral of the following Equation of Mixed Differences:-
The general integral itself is of the form,
and it is worthy of remark, that the engine might (in a manner more or less similar to the preceding) calculate the value of this formula upon most other hypotheses for the functions in the integral with as much, or (in many cases) with more ease than it can formula (8.). A. A. L.
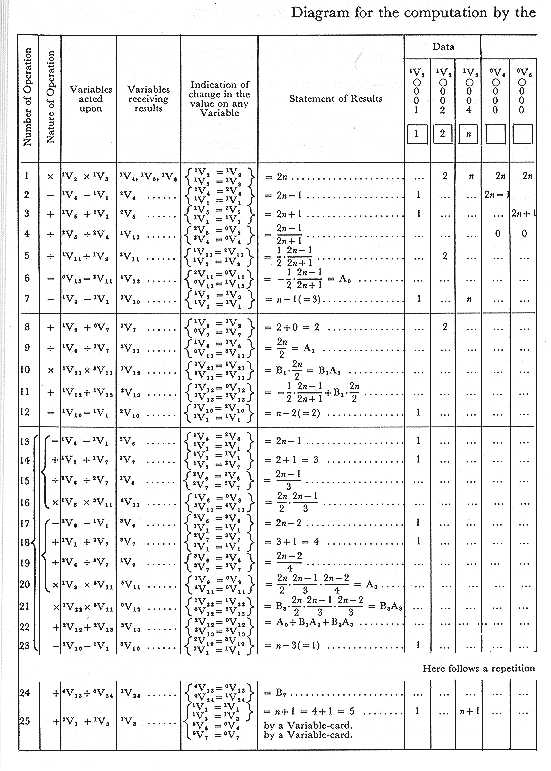
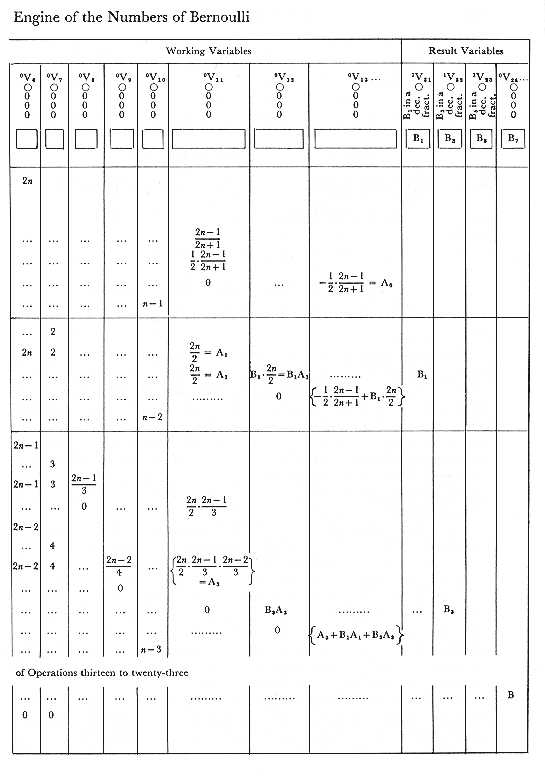
[2] In fact, such an extension as we allude to would merely constitute a further and more perfected development of any system introduced for making the proper combinations of the signs plus and minus. How ably M. Menabrea has touched on this restricted case is pointed out in Note B.
[3] The machine might have been constructed so as to tabulate for a higher value of n than seven. Since, however, every unit added to the value of n increases the extent of the mechanism requisite, there would on this account be a limit beyond which it could not be practically carried. Seven is sufficiently high for the calculation of all ordinary tables.
The fact that, in the Analytical Engine, the same extent of mechanism suffices for the solution of Dn uz = 0, whether n = 7, n = 100,000, or n = any number whatever, at once suggests how entirely distinct must be the nature of the principles through whose application matter has been enabled to become the working agent of abstract mental operations in each of these engines respectively; and it affords an equally obvious presumption, that in the case of the Analytical Engine, not only are those principles in themselves of a higher and more comprehensive description, but also such as must vastly extend the practical value of the engine whose basis they constitute.
[4] This subject is further noticed in Note F.
[2] This adjustment is done by hand merely.
[3] It is convenient to omit the circles whenever the signs + or - can be actually represented.
[2] We recommend the reader to trace the successive substitutions backwards from (1.) to (4.), in Mons. Menabrea's Table. This he will easily do by means of the upper and lower indices, and it is interesting to observe how each V successively ramifies (so to speak) into two other V's in some other column of the Table, until at length the V's of the original data are arrived at.
[3] See note, page 34. [immediately above]
[2] This division would be managed by ordering the number 2 to appear on any separate new column which should be conveniently situated for the purpose, and then directing this column (which is in the strictest sense a Working-Variable) to divide itself successively with V32, V33, &c.
[3] It should be observed, that were the rest of the factor (A + A cos q + &c.) taken into account, instead of four terms only, C3 would have the additional term 1/2 B1 A4; and C4 the two additional terms, B A4, 1/2 B1 A5. This would indeed have been the case had even six terms been multiplied.
[4] Classics Editor's note: In the original text, a vinculum appears over "B A1 + B1 A + 1/2 B1 A2" in the equation "( B A + 1/2 B1 A1) + (B A1 + B1 A + 1/2 B1 A2 . cos q)". In the present text, the vinculum has been substituted with parentheses.
[5] Classics Editor's note: In the original text, a vinculum appears over "An - 1 + An + 2" in the equation "(B An + 1/2 B1 . An - 1 + An + 2) cos n q". In the present text, the vinculums have been substituted with parentheses.
[6] A cycle that includes n other cycles, successively contained one within another, is called a cycle of the n + 1th order. A cycle may simply include many other cycles, and yet only be of the second order. If a series follows a certain law for a certain number of terms, and then another law for another number of terms, there will be a cycle of operations for every new law; but these cycles will not be contained one within another, - they merely follow each other. Therefore their number may be infinite without influencing the order of a cycle that includes a repetition of such a series.
[7] Classics Editor's note: In the original text, vinculums appear over "p - 1" and "p - n" in the equation "p (1, 2, . . m), p - 1 (1, 2 . . .m), p - 2 (1, 2 . . m) . . . p - n (1, 2 . . m). In the present text, the vinculums have been substituted with parentheses.
[2] The engine cannot of course compute limits for perfectly simple and uncompounded functions, except in this manner. It is obvious that it has no power of representing or of manipulating with any but finite increments or decrements; and consequently that wherever the computation of limits (or of any other functions) depends upon the direct introduction of quantities which either increase or decrease indefinitely, we are absolutely beyond the sphere of its powers. Its nature and arrangements are remarkably adapted for taking into account all finite increments or decrements (however small or large), and for developing the true and logical modifications of form or value dependent upon differences of this nature. The engine may indeed by considered as including the whole Calculus of Finite Differences; many of whose theorems would be especially and beautifully fitted for development by its processes, and would offer peculiarly interesting considerations. We may mention, as an example, the calculation of the Numbers of Bernoulli by means of the Differences of Zero.
[3] See the diagram at the
end of these Notes.
[4] Classics Editor's note: In the original text, a vinculum appears over "n + 2" in the equation "(n + 2 - 3)". In the present text, the vinculum has been substituted with parentheses.
[5] It is interesting to observe, that so complicated a case as this calculation of the Bernoullian Numbers nevertheless presents a remarkable simplicity in one respect; viz. that during the processes for the computation of millions of these Numbers, no other arbitrary modification would be requisite in the arrangements, excepting the above simple and uniform provision for causing one of the data periodically to receive the finite increment unity.