
(Return to Classics index)
First published as Untersuchungen zur Lehre von der Gestalt II, in Psycologische Forschung, 4, 301-350. Translation published in Ellis, W. (1938). A source book of Gestalt psychology (pp. 71-88). London: Routledge & Kegan Paul.[1]
I stand at the window and see a house, trees, sky.
Theoretically I might say there were 327 brightnesses and nuances of colour. Do I have "327"? No. I have sky, house, and trees. It is impossible to achieve "327 " as such. And yet even though such droll calculation were possible and implied, say, for the house 120, the trees 90, the sky 117 -- I should at least have this arrangement and division of the total, and not, say, 127 and 100 and 100; or 150 and 177.
The concrete division which I see is not determined by some arbitrary mode of organization lying solely within my own pleasure; instead I see the arrangement and division which is given there before me. And what a remarkable process it is when some other mode of apprehension does succeed! I gaze for a long time from my window, adopt after some effort the most unreal attitude possible. And I discover that part of a window sash and part of a bare branch together compose an N.
Or, I look at a picture. Two faces cheek to cheek. I see one (with its, if you will, "57" brightnesses) and the other ("49" brightnesses). I do not see an arrangement of 66 Plus 40 nor of 6 plus 100 There have been theories which would require that I see "106". In reality I see two faces !
Or, I hear a melody (17 tones) with its accompaniment (32 tones). I hear the melody and accompaniment, not simply "49"and certainly not 20 plus 29. And the same is true even in cases where there is no stimulus continuum. I hear the melody and its accompaniment even when they are played by an old-fashioned clock where each tone is separate from the others. Or, one sees a series of discontinuous dots upon a homogeneous ground not as a sum of dots, but as figures. Even though there may here be a greater latitude of possible arrangements, the dots usually combine in some "spontaneous", "natural" articulation -- and any other arrangement, even if it can be achieved, is artificial and difficult to maintain.
When we are presented with a number of stimuli we do not as a rule experience "a number" of individual things, this one and that and that. Instead larger wholes separated from and related to one another are given in experience ; their arrangement and division are concrete and definite.
Do such arrangements and divisions follow definite principles? When the stimuli abcde appear together what are the principles according to which abc/de and not ab/cde is experienced ? It is the purpose of this paper to examine this problem, and we shall therefore begin with cases of discontinuous stimulus constellations.
I. A row of dots is presented upon a homogeneous ground. The alternate intervals are 3 mm. and 12 mm.

Normally this row will be seen as ab/cd, not as a/bc/de. As a matter of fact it is for most people impossible to see the whole series simultaneously in the latter grouping.
We are interested here in what is actually seen. The following will make this clear. One sees a row of groups obliquely tilted from lower left to upper right (ab/cd/ef). The arrangement a/bc/de is extremely difficult to achieve. Even when it can be seen, such an arrangement is far less certain than the other and is quite likely to be upset by eye-movements or variations of attention.
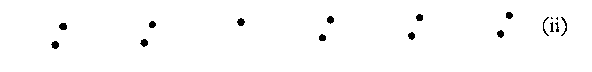
This is even more clear in (iii).
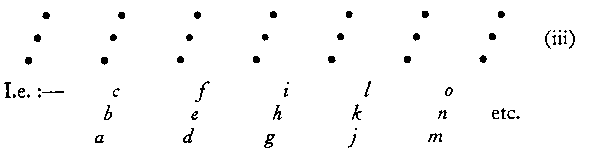
Quite obviously the arrangement abc/def/ghi is greatly superior to ceg/fhj/ikm.
Another, still clearer example of spontaneous arrangement is that given in (iv). The natural grouping is, of course, a/bcd/efghi, etc.

Resembling (i) but still more compelling is the row of three-dot groupings given in (v). One sees abc/def, and not some other (theoretically possible) arrangement.
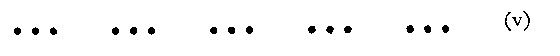
Another example of seeing what the objective arrangement dictates is contained in (vi) for vertical, and in (vii) for horizontal groupings.
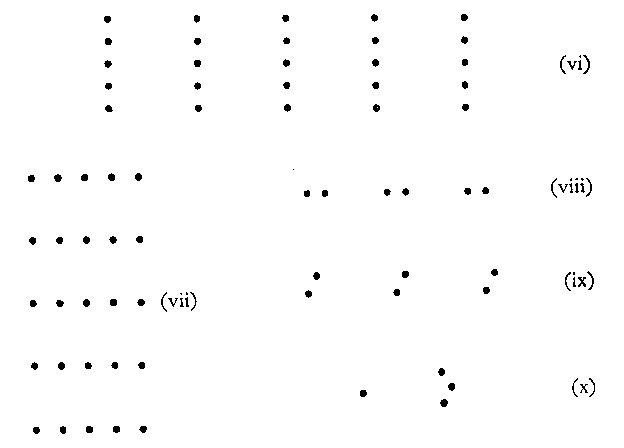
In all the foregoing cases we have used a relatively large number of dots for each figure. Using fewer we find that the arrangement is not so imperatively dictated as before, and reversing the more obvious grouping is comparatively easy. Examples: (viii)-(x).
It would be false to assume that (viii)-(x) lend themselves more readily to reversal because fewer stimulus points (dots) are involved. Such incorrect reasoning would be based upon the proposition "The more dots, the more difficult it will be to unite them into groups." Actually it is only the unnatural, artificial arrangement which is rendered more difficult by a larger number of points. The natural grouping (cf., e.g., (i), (ii), etc.) is not at all impeded by increasing the number of dots. It never occurs, for example, that with a long row of such dots the process of "uniting" them into pairs is abandoned and individual points seen instead. It is not true that fewer stimulus points " obviously " yield simpler, surer, more elementary results.
In each of the above cases that form of grouping is most natural which involves the smallest interval. They all show, that is to say, the predominant influence of what we may call The Factor of Proximity. Here is the first of the principles which we undertook to discover. That the principle holds also for auditory organization can readily be seen by substituting tap-tap, pause, tap-tap, pause, etc. for (i), and so on for the others.
II. Proximity is not, however, the only factor involved in natural groupings. This is apparent from the following examples. We shall maintain an identical proximity throughout but vary the colour of the dots themselves:--
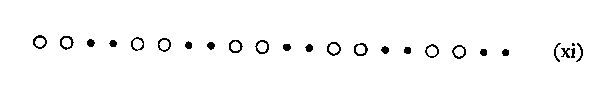
Or, again:--
Or, to repeat (v) but with uniform proximity :--
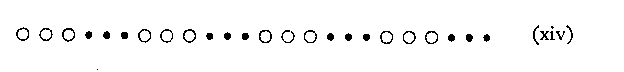
Thus we are led to the discovery of a second principle --viz. the tendency of like parts to band together -- which we may call The Factor of Similarity. And again it should be remarked that this principle applies also to auditory experience. Maintaining a constant interval, the beats may be soft and loud (analogous to (xi)) thus: . . ! ! . . ! ! etc. Even when the attempt to hear some other arrangement succeeds, this cannot be maintained for long. The natural grouping soon returns as an overpowering "upset" of the artificial arrangement.
In (xi)-(xiv) there is, however, the possibility of another arrangement which should not be overlooked. We have treated these sequences in terms of a constant direction from left to right. But it is also true that a continual change of direction is taking place between the groups themselves : viz. the transition from group one to group two (soft-to-loud), the transition from group two to group three (loud-to-soft), and so on. This naturally involves a special factor. To retain a constant direction it would be necessary to make each succeeding pair louder than the last. Schematically this can be represented as :--

Or, in the same way:--
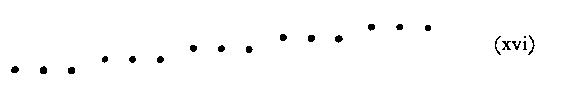
This retention of constant direction could also be demonstrated with achromatic colours (green background) thus: white, light grey, medium grey, dark grey, black. A musical reproduction of (xv) would be C, C, E, E, F#, F#, A, A, C, C, . . .; and similarly for (xvi) : C, C, C, E, E, E, F#, F#, F#, A, A, A, C, C, C, . . .
Thus far we have dealt merely with a special case of the general law. Not only similarity and dissimilarity, but more and less dissimilarity operate to determine experienced arrangement. With tones, for example, C, C#, E, F, G#, A, C, C# . . . will be heard in the grouping ab/cd . . . and C, C#, D, E, F, F#, G#, A, A#, C, C#, D. . . in the grouping abc/def . . . Or, again using achromatic colours, we might present these same relationships in the manner suggested (schematically) by (xvii) and (xviii).


(It is apparent from the foregoing that quantitative comparisons
can be made regarding the application of the same laws in regions
-- form, colour, sound -- heretofore treated as psychologically
separate and heterogeneous.)
III. What will happen when two such factors appear in the same constellation ? They may be made to cooperate ; or, they can be set in opposition-as, for example, when one operates to favour ab/cd while the other favours /bc/de. By appropriate variations, either factor may be weakened or strengthened. As an example, consider this arrangement:--
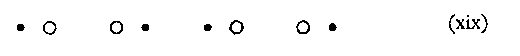
where both similarity and proximity are employed. An illustration of opposition in which similarity is victorious despite the preferential status given to proximity is this .-
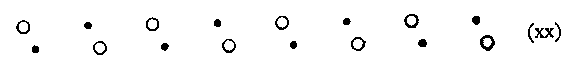
A less decided victory by similarity:--

Functioning together towards the same end, similarity and proximity greatly strengthen the prominence here of verticality:--

Where, in cases such as these, proximity is the predominant factor, a gradual increase of interval will eventually introduce a point at which similarity is predominant. In this way it is possible to test the strength of these Factors.
IV. A row of dots is presented:--
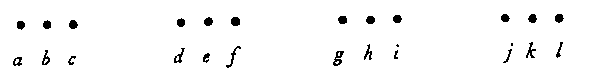
and then, without the subject's expecting it, but before his eyes, a sudden, slight shift upward is given, say, to d, e, f or to d, e, f and j, k, l together. This shift is "pro-structural", since it involves an entire group of naturally related dots. A shift upward of, say, c, d, e or of c, d, e and i, j, k would be "contra-structural" because the common fate (i.e. the shift) to which these dots are subjected does not conform with their natural groupings.
Shifts of the latter kind are far less "smooth" than those of the former type. The former often call forth from the subject no more than bare recognition that a change has occurred; not so with the latter type. Here it is as if some particular "opposition" to the change had been encountered. The result is confusing and discomforting. Sometimes a revolt against the originally dominant Factor of Proximity will occur and the shifted dots themselves thereupon constitute a new grouping whose common fate it has been to be shifted above the original row. The principle involved here may be designated The Factor of Uniform Destiny (or of "Common Fate").
V. Imagine a sequence of rows of which this would be the first :-
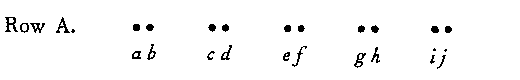
The intervals between a-b, c-d, etc. (designated hereafter as S1) are in this row 2 mm.; those between b-c, d-e, etc. (S2) are 20 mm. We shall hold a, c, e, g, and i constant while varying the horizontal position of b, d, f, h, and j thus:--
| Row A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
| G |
Experimentally we now present these rows separately.[2] It will be found that there are three major constellations : The dominant impression in Row A is ab/cd, and in Row G it is /bc/de. But in the middle row (represented in our schema by D) the predominant impression is that of uniformity. These three constellations thus constitute "unique regions" and it will be found that intervening rows are more indefinite in character and their arrangement less striking; indeed they are often most easily seen in the sense of the nearest major constellation. Example: intermediate rows in the vicinity of D will be seen as "not quite equally spaced" (even when the difference between intervals S1 and S2 is clearly supraliminal).
Or to take another example. Suppose one side of an angle is held horizontal and the other passes through an arc from 30 to 150 No more here than in the preceding case is each degree of equal value psychologically. Instead there are three principal stages: acute, right, and obtuse. The "right angle", for example, has a certain region such that an angle of 93 appears as a (more or less inadequate) right angle. Stages intermediate between the major ones have the character of indefiniteness about them and are readily seen in the sense of one or the other adjacent Prägnanzstufen[3]. This can be very clearly demonstrated by tachistoscopic presentations, for in this case the observer frequently sees a right angle even when objectively a more acute or more obtuse angle is being presented. Although the observer may report that it was "not quite correct", "somehow wrong", etc., he is usually unable to say in which direction the "error" lies.
In general we may say, as in the case above where the location
of b between a and c was varied, that our
impressions are not psychologically equivalent for all positions
of b. Instead there are certain Prägnanzstufen
with their appropriate realms or regions, and intermediate
stages typically appear "in the sense of" one of these
characteristic regions.
VI. Suppose now that the variations from A to G are carried out before the observer's eyes. This procedure leads to a discovery of The Factor of Objective Set [Einstellung]. As one proceeds from A towards G or from G towards A the original grouping in each case (i.e. ab/cd in the former, /bc/de in the latter) tends to maintain itself even beyond the middle row. Then there occurs an upset and the opposite grouping becomes dominant. The constellation of Row C, for example, will be different when preceded by A and B from what it would be when preceded by G, F, E. This means that the row is a part in a sequence and the law of its arrangement is such that the constellation resulting from one form of sequence will be different from that given by some other sequence. Or, again, a certain (objectively) ambiguous arrangement will be perfectly definite and unequivocal when given as a part in a sequence. (In view of its great strength this Factor must in all cases be considered with much care.)
Parenthetically: it is customary to attribute influences such as these to purely subjective (meaning by this "purely arbitrary") conditions. But our examples refer only to objective factors : the presence or absence of a certain row of dots in a sequence is determined solely by objective conditions. It is objectively quite different whether a Row M is presented after Row L or after Row N; or, whether the presentations follow one another immediately or occur on different days.
When several rows are simultaneously presented it is of course possible to select one row or another quite according to one's (subjective) fancy; or any certain row may be compared with another just above or below it. But this special case is not what we are here concerned with. Such subjectively determined arrangements are possible only if the rows of dots permit of two or more modes of apprehension. Curiously enough, however, it has been just this special case (where objective conditions do not themselves compel us to see one arrangement rather than another) which has usually been thought of as the fundamental relationship. As a matter of fact we shall see below how even purely subjective factors are by no means as arbitrary in their operations as one might suppose.
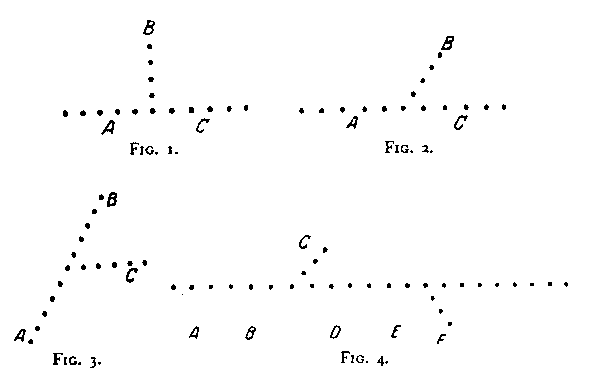
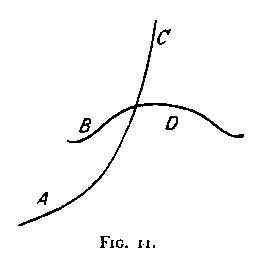
VII. That spatial proximity will not alone account for organization can be shown by an example such as Fig. 1. Taken individually the points in B are in closer proximity to the individual points of A.
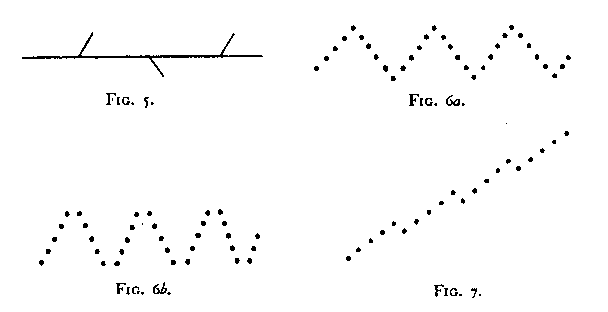
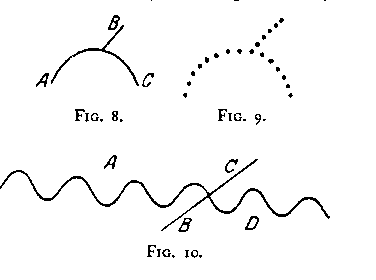
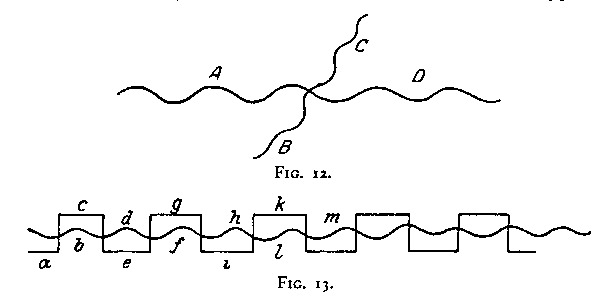
(or C) than the points of 4 and C are to each other. Nevertheless the perceived grouping is not AB/C of BC/A¸ but, quite clearly "a horizontal line and a vertical line" -- i.e. AC/B. In Fig. 2 the spatial proximity of B and C is even greater, yet the result is still AC/B i.e. horizontal-oblique. The same is true of the relationship ,AB/C in Fig. 3. As Figs. 4-7 also show we are dealing now with a new principle which we may call The Factor of Direction. That direction may still be unequivocally given even when curved lines are used is of course obvious (cf. Figs. 8-12).
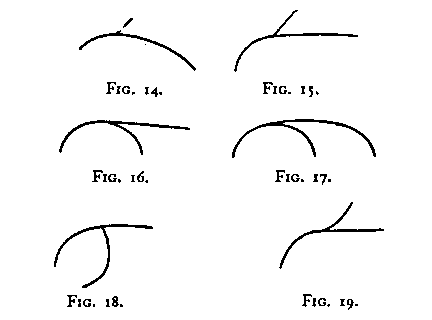
The dominance of this Factor in certain cases will be especially clear if one attempts to see Fig. 13 as (abefil…) (cdghkm...) instead of (acegik...) (bdfhlm...).
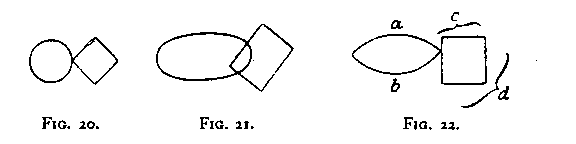
Suppose in Fig. 8 we had only the part designated as A, and suppose any two other lines were to be added. Which of the additional ones would join, A as its continuation and which would appear as an appendage?
As it is now drawn, AC constitutes the continuity, B the appendage. Figs. 14-19 represent a few such variations. Thus, for example, we see that AC/B is still the dominant organization even in Fig. 15 (where C is tangent to the circle implied by A).
But in Fig. 16, when B is tangent to A, we still have AC/B. Naturally, however, the length of B and C is an important consideration. In all such cases there arise the same questions as those suggested above in our discussion of Prägnanzstufen. Certain arrangements are stronger than others, and seem to "triumph"; intermediate arrangements are less distinctive, more equivocal.
On the whole the reader should find no difficulty in seeing what is meant here. In designing a pattern, for example, one has a feeling how successive parts should follow one another; one knows what a "good" continuation is, how "inner coherence" is to be achieved, etc.; one recognizes a resultant "good Gestalt" simply by its own "inner necessity". A more detailed study at this juncture would require consideration of the following: Additions to an incomplete object (e.g. the segment of a curve) may proceed in a direction opposed to that of the original, or they may carry on the principle "logically demanded" by the original.
It is in the latter case that "unity" will result. This does not mean, however, that "simplicity" will result from an addition which is (piecewise considered) "simple". Indeed even a very "complicated" addition may promote unity of the resultant whole. "Simplicity" does not refer to the properties of individual parts ; simplicity is a property of wholes. Finally, the addition must be viewed also in terms of such characteristic "whole properties" as closure, equilibrium, and symmetry.[4]
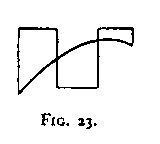
From an inspection of Figs. 20-22 we are led to the discovery of still another principle: The Factor of Closure. If A, B, C, D are given and AB/CD constitute two self-enclosed units, then this arrangement rather than AC/BD will be apprehended. It is not true, however, that closure is necessarily the dominant Factor in all cases which satisfy these conditions. In Fig. 23, for example, it is not three self-enclosed areas but rather The Factor of the "Good Curve" which predominates.
It is instructive in this connection to determine the conditions under which two figures will appear as two independent figures, and those under which they will combine to yield an entirely different (single) figure. (Examples: Figs. 24-27). And this applies also to surfaces.[5] The reader may test the influence of surface wholeness by attempting to see Fig. 24 as three separate, closed figures. With coloured areas the unity of naturally coherent parts may be enhanced still more.
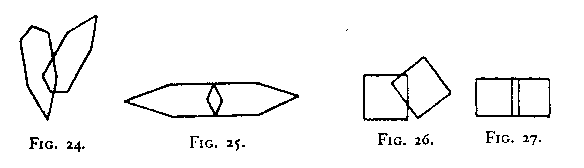
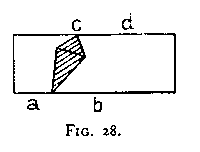
Fig. 28 is most readily seen as an oblique deltoid (bc) within a rectangle (ad). Try now to see on the left side a hexagon whose lower right-hand corner is shaded, and on the right side another hexagon whose upper left-hand corner is shaded [viz. Figs. 28a and 28b].
Once more we observe (as with the curves of Figs. 9-12) the influence of a tendency towards the "good" Gestalt, and in the present case it is probably easier than before to grasp the meaning of this expression. Here it is clearly evident that a unitary colour tends to bring about uniformity of colouring within the given surface.[6]
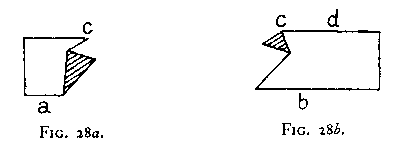
Taking any figure (e.g. Fig. 29) it is instructive to raise such questions as the following: By means of what additions can one so alter the figure that a spontaneous apprehension of the original would be impossible? (Figs. 30-32 are examples.) An excellent method of achieving this result is to complete certain "good subsidiaries" in a manner which is "contra-structural" relative to the original. (But notice that not all. additions to the original will have this effect. Figs. 33-34, for example, represent additions which we may call "indifferent" since they are neither "prostructural" nor "contra-structural".)
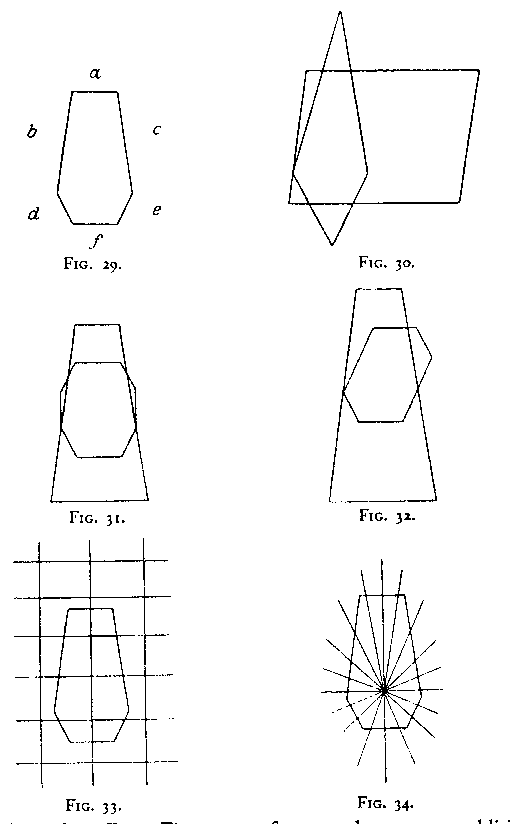
Let us call the original (Fig. 29) O and any contra-structural
addition C, while any pro-structural addition we shall
call P. For our purposes, then, O is to be thought
of as a subsidiary of some more inclusive whole. Now O
whether taken alone or as part of OP is different from
what it would be in OC It is of the first importance for
O in which constellation it appears.[7]
(In this way a person thoroughly familiar with 0 can be made quite
blind to its existence. This applies not only to recognition
but to perception in general.)
VIII. Another Factor is that of past experience or habit. Its principle is that if AB and C but not BC have become habitual (or "associated ") there is then a tendency for ABC to appear as AB/C. Unlike the other principles with which we have been dealing, it is characteristic of this one that the contents A, B, C are assumed to be independent of the constellation in which they appear. Their arrangement is on principle determined merely by extrinsic circumstances (e.g. drill).
There can be no doubt that some of our apprehensions are determined in this way.[8] Often arbitrary material can be arranged in arbitrary form and, after a sufficient drill, made habitual. The difficulty is, however, that many people are inclined to attribute to this principle the fundamental structure of all apprehension. The situation in Sec. VII, they would say, simply involves the prominence of habitual complexes. Straight lines, right angles, the arcs of circles, squares-all are familiar from everyday experience. And so it is also with the intervals between parts (e.g. the spaces between written words), and with uniformity of coloured surfaces. Experience supplies a constant drill in such matters.
And yet, despite its plausibility, the doctrine of past experience brushes aside the real problems of apprehension much too easily. Its duty should be to demonstrate in each of the foregoing cases (1) that the dominant apprehension was due to earlier experience (and to nothing else); (2) that non-dominant apprehensions in each instance had not been previously experienced ; and, in general, (3) that in the amassing of experience none but adventitious factors need ever be involved. It should be clear from our earlier discussions and examples that this programme could not succeed. A single example will suffice to show this. Right angles surround us from childhood (table, cupboard, window, comers of rooms, houses). At first this seems quite self-evident. But does the child's environment consist of nothing but man-made objects? Are there not in nature (e.g. the branches of trees) fully as many obtuse and acute angles ? But far more important than these is the following consideration. Is it true that cupboards, tables, etc., actually present right angles to the child's eye? If we consider the literal reception of stimuli upon the retina, how often are right angles as such involved? Certainly less often than the perception of right angles. As a matter of fact the conditions necessary for a literal "right angle" stimulation are realized but rarely in everyday life (viz. only when the table or other object appears in a frontal parallel plane). Hence the argument from experience is referring. not to repetition of literal stimulus conditions, but to repetition of phenomenal experience and the problem therefore simply repeats itself.
Regardless of whether or not one believes that the relationships discussed in Sec. VII depend upon past experience, the question remains in either case: Do these relationships exhibit the operations of intrinsic laws or not, and if so, which laws? Such a question requires experimental inquiry and cannot be answered by the mere expression "past experience".
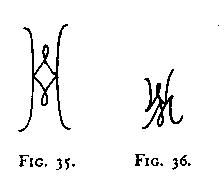
Let us take two arrangements which have been habitually experienced in the forms abc and def many thousands of times. I place them together and present abcdef. Is the result sure to be abcldef? Fig. 35, which is merely the combination of a W and an M, may be taken as an example. One ordinarily sees not the familiar letters W and M, but a sinuation between two symmetrically curved uprights. If we designate parts of the W from left to right as abc and those of the M as def, the figure may be described as ad/be/cf (or as /be/ between /ad/ and /cf/); not, however, as abc/def.
But the objection might be raised that while we are familiar enough with W and M, we are not accustomed to seeing them in this way (one above the other) and that this is why the other arrangement is dominant. It would certainly be false, however, to consider this an "explanation". At best this mode of approach could show only why the arrangement W-M is not seen; the positive side would still be untouched. But apart from this, the objection is rendered impotent when we arrange abc and def one above the other (Fig. 36) in a fashion quite as unusual as that given in Fig- 35. Nor is the argument admissible that the arrangements /ad/ and /be/ and /cf/ in Fig. 35 are themselves familiar from past experience. It simply is not true that as much experience has been had with /be/ as with the b in abc and the e in def.
IX. When an object appears upon a homogeneous field there must be stimulus differentiation (inhomogeneity) in order that the object may be perceived. A perfectly homogeneous field appears as a total field [Ganzfeld] opposing subdivision, disintegration, etc. To effect a segregation within this field requires relatively strong differentiation between the object and its background. And this holds not only for ideally homogeneous fields but also for fields in which, e.g., a symmetrical brightness distribution obtains, or in which the "homogeneity" consists in a uniform dappled effect. The best case for the resulting of a figure in such a field is when in the total field a closed surface of simple form is different in colour from the remaining field. Such a surface figure is not one member of a duo (of which the total field or "ground" would be the other member) ; its contours serve as boundary lines only for this figure. The background is not limited by !he figure, but usually seems to continue unbroken beneath that figure.
Within this figure there may be then further subdivision resulting in subsidiary wholes. The procedure here as before is in the direction "from above downward" and it will be found that the Factors discussed in Sec. VII are crucial for these subdivisions.[9] As regards attention, fixation, etc., it follows that they are secondarily determined relative to the natural relations already given by whole constellations as such. Consider, e.g., the difference between some artificially determined concentration of attention and that spontaneously resulting from the pro-structural emphasis given by a figure itself. For an approach "from above downward", i.e. from whole-properties downward towards subsidiary wholes and parts, individual parts ("elements") are not primary, not pieces to be combined in and-summations, but are parts of wholes.
Footnotes
1 Grateful acknowledgment is hereby made to Julius Springer, Verlagsbuchhandlung, Berlin, for permission to reproduce the illustrations used in this SELECTION.
2 The above classification of but 7 rows is intended merely as a schema. In actual experimentation many more than 7 (with correspondingly more minute variations of intervals) are needed.
3 ["Stufen" = steps or stages ; the term "Prägnanz" cannot be translated. In the present usage "Prägnanzstufen" means regions of figural stability in a sense which should be clear from the text.]
4 Symmetry signifies far more than mere similarity of parts; it refers rather to the logical correctness of a part considered relative to the whole in which that part occurs.
5 Compare in Selection 6 ["On transparency", in Ellis, W. (Ed.) (1938). A source book of Gestalt psychology (pp. 89-94). London: Routledge & Kegan Paul] the application which [Wilhelm] Fuchs makes of this.
6 The Factor of similarity can thus be seen as a special instance of The Factor of the Good Gestalt.
7 Compare Selections 9a and 9b [Kurt Gottschaldt's "Gestalt factors and repetition" (2 parts). In W. Ellis (Ed.) (1938). A source book of Gestalt psychology (pp. 89-94). London: Routledge & Kegan Paul]
8 Example: 314 cm. is apprehended as abc/de, not as ab/cde -- i.e. as 314 cm., not 31/4 cm. nor as 314c/m.
9 Epistemologically this distinction between
"above" and "below" is of great importance.
The mind and the psychophysiological reception of stimuli do not
respond after the manner of a mirror or photographic apparatus
receiving individual 1. stimuli " qua individual units
and working them up "from below" into the objects of
experience. Instead response is made to articulation as a whole-and
this after the manner suggested by the Factors of Sec. VII. It
follows that the apparatus of reception cannot be described as
a piecewise sort of mechanism. It must he of such a nature as
to he able to grasp the inner necessity of articulated
wholes. When we consider the problem in this light it becomes
apparent that pieces are not even experienced as such but that
apprehension itself is characteristically "from above".