Classics in the History of Psychology
An internet resource developed by
Christopher D. Green
ISSN 1492-3713
(Return to index)
On Small Differences in Sensation
By Charles Sanders Peirce & Joseph Jastrow (1885)
First published in Memoirs
of the
Presented
Posted Jan 2005
Editor's note: Thanks to Joseph M. Ransdell of
The physiological psychologists assume that two nerve excitations alike in quality will only produce distinguishable sensations provided they differ in intensity by an amount greater than a fixed ratio. The least perceptible difference of the excitations divided by half their sum is what they call the Unterschiedsschwelle. Fechner[1] gives an experiment to prove the fact assumed, namely: He finds that two very dim lights placed nearly in line with the edge of an opaque body show but one shadow of the edge. It will be found, however, that this phenomenon is not a clearly marked one, unless the lights are nearly in range. If the experiment is performed with lateral shifting of one of the lights, and with a knowledge of the effects of a telescope upon the appearance of terrestrial objects at night, it will be found very far from conclusive.
The conception of the psychologists is certainly a difficult one to seize. According to their own doctrine, in which the observed facts seem fully to bear them out, the intensity of the sensation increases continuously with the excitation, so that the least increase of the latter must produce a corresponding increase of the former. And, indeed, the hypothesis that a continuous increase of the excitation would be accompanied by successive discrete increments of the sensation, gratuitous as it would be, would not be sufficient to account for a constant Unterschiedsschwelle. We are therefore forced to conclude that if there be such a phenomenon, it has its origin, not in the faculty of sensation, but in that of comparing sensations. In short, if the phenomenon were established, we should be forced to say that there was a least perceptible difference of sensation -- a difference which, though existing in sensation, could not be brought into consciousness by any effort of attention. But the errors of our judgments in comparing our sensations seem sufficiently accounted for by the slow and doubtless complicated process by which the impression is conveyed from the periphery to the brain; for this must be liable to more or less accidental derangement at every step of its progress. Accordingly we find that the frequencies of errors of different magnitudes follow the probability curve, which is the law of an effect brought about by the sum of an infinite number of infinitesimal causes. This theory, however, does not admit of an Unterschiedsschwelle. On the contrary, it leads to the method of least squares, according to which the multiplication of observations will indefinitely reduce the error of their mean, so that if of two excitations one were ever so little the more intense, in the long run it would be judged to be the more intense the majority of times. It is true that the astronomers themselves have not usually supposed that this would be the case, because (apart from constant errors, which have no relevancy to the present question) they have supposed this extreme result to be contrary to common sense. But it has seemed to us that the most satisfactory course would be to subject the question to the test of direct experiment. If there be a least perceptible difference, then when two excitations differing by less than this are presented to us, and we are asked to judge which is the greater, we ought to answer wrong as often as right in the long run. Whereas, if the theory of least squares is correct, we not [p. 76] only ought to answer right oftener than wrong, but we ought to do so in a predictable ratio of cases.[2]
We have experimented with the pressure sense, observing the proportion of errors among judgments as to which is the greater of two pressures, when it is known that the two are two stated pressures, and the question presented for the decision of the observer is, which is which? From the probability, thus ascertained, of committing an error of a given magnitude, the probable error of a judgment can be calculated according to the mathematical theory of errors. If, now, we find that when the ratio of the two pressures is smaller than a certain ratio, the erroneous judgments number one-half of the whole, while the mathematical theory requires them to be sensibly fewer, then this theory is plainly disproved, and the maximum ratio at which this phenomenon is observed the so-called Unterschiedsschwelle. If, on the other hand, the values obtained for the probable error are the same for errors varying from three times to one-fourth of the probable error (the smallest for which it is easy to collect sufficient observations), then the theory of the method of least squares is shown to hold good within those limits, the presumption will be that it extends still further, and it is possible that it holds for the smallest differences of excitation. But, further, if this law is shown to hold good for difference so slight that the observer is not conscious of being able to discriminate between the sensations at all, all reason for believing in an Unterschiedsschwelle is destroyed. The mathematical theory has the advantage of yielding conceptions of greater definiteness than that of the physiologists, and will thus tend to improve methods of observation. Moreover, it affords a ready method for determining the sensibility or fineness of perception and allows of a comparison of one observer's results with the results of others; for, knowing the number of errors in a certain number of experiments, and accepting the conclusions of this paper, the calculated ratio to the total excitation of that variation of excitation, in judging which we should err one time out of four, measures the sensibility. Incidentally our experiments will afford additional information upon the value of the normal average sensibility for the pressure sense, which they seem to make a finer sense than it has hitherto been believed to be. But in this regard two things have to be noted: (1) Our value relates to the probable error or the value for the point at which an error is committed half the time; (2) in our experiments there were two opportunities for judging, for the initial weight was either first increased and then diminished, or vice versa, the subject having to say which of these two double changes was made. It would seem at first blush that the value thus obtained ought to be multiplied by √2(1.414) to get the error of a single judgment. Yet this would hardly be correct, because the judgment, in point of fact, depended almost exclusively on the sensation of increase of pressure, the decrease being felt very much less. The ratio √2(1.414) would therefore be too great, and 1.2 would perhaps be about correct. The advantage of having two changes in one experiment consists in this: If only one change were employed, then some of the experiments would have an increase of excitation only and the others a decrease only; and since the former would yield a far greater amount of sensation than the latter, the nature of the results would be greatly complicated; but when each experiment embraces a [p. 77]double change this difference in the amount of sensation caused by an increase and decrease of pressure affects every experiment alike, and the liability to error is constant.[3]
Throughout our observations we noted the degree of confidence with which the observer gave his judgment upon a scale of four degrees, as follows:
0
denoted absence of any preference for one answer over its opposite, so that it
seemed nonsensical to answer at all.
1 denoted a distinct leaning to one alternative.
2 denoted some little confidence of being right.
3 denoted as strong a confidence as one would have about such sensations.
We do not mean to say that when zero was the recorded confidence, there was absolutely no sensation of preference for the answer given. We only mean that there was no sensation that the observer noticed when attending to his feelings of this sort as closely as he conveniently could, namely, closely enough to mark them on this scale. The scale of confidence fluctuated considerably. Thus, when Mr. Jastrow passed from experiments upon differences of weight of 60, 30, and 15 on the thousand to differences of 20, 10, and 5 on the thousand, although the accuracy of his judgments was decidedly improved, his confidence fell off very greatly, owing to his no longer having the sensation produced by a difference of 60 present to his memory. The estimations of confidence were also rough, and might be improved in future work. The average marks seem to conform to the formula--
m = c log (p/1-p)
where m denotes the degree of confidence on the scale, p denotes the probability of the answer being right, and c is a constant which may be called the index of confidence.
To show that this formula approximates to the truth, we compare it with the average marks assigned to estimates of differences for which more than a hundred experiments were made. Mr. Jastrow's experiments are separated into groups, which will be explained below.
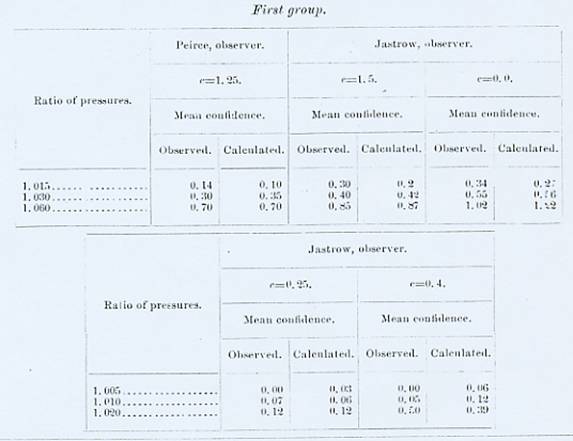
[p.
78]
The judgments enunciated with any given degree of confidence were more likely
to be right with greater differences than with smaller differences. To show
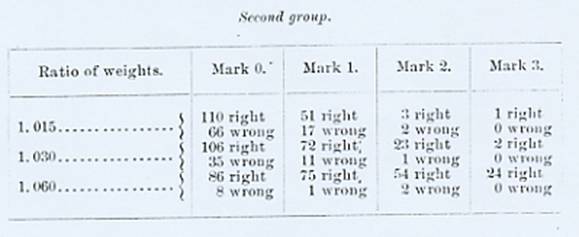
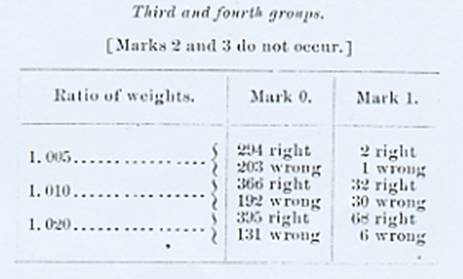
this, we give the frequency of the different marks in Mr. Jastrow's second,
third, and fourth groups.[4]
[Editor's note: The table immediately below is misplaced within footnote 4 in the original publication. -cdg-]
The
apparatus used was an adaptation of a "
The observations were conducted in the following manner: At each sitting three differential weights were employed. At first we always began and ended with the heaviest, but at a later period the plan was to begin on alternate days with the lightest and heaviest. When we began with the heaviest 25 observations [5] were made with that; then 25 with the middle one, and then 25 with the lightest; this constituted one-half of the sitting. It was completed by three more sets of 25, the order of the weights being reversed. When we began with the lightest the heaviest was used for the third and fourth sets. In this way 150 experiments on each of us were taken at one sitting of two hours.
A pack of 25 cards were taken, 12 red and 13 black, or vice versa, so that in the 50 experiments made at one sitting with a given differential weight, 25 red and 25 black cards should be used. These cards were cut exactly square and their corners were distinguished by holes punched in them so as to indicate the scale of numbers (0, 1, 2, 3) used to designate the degree of confidence of the judgment. The backs of these cards were distinguished from their faces. They were, in fact, made of ordinary playing-cards. At the beginning of a set of 25, the pack was well shuffled, and, the operator and subject having taken their places, the operator was governed by the color [p. 80] of the successive cards in choosing whether he should first diminish the weight and then increase it, or vice versa. If the weight was to be first increased and then diminished the operator brought the pressure exerted by the kilogram alone upon the finger of the subject by means of the lever and cam mentioned above, and when the subject said "change" he gently lowered the differential weight, resting in the small pan, upon the pan of the balance. The subject, having appreciated the sensation, again said "change," whereupon the operator removed the differential weight. If, on the other hand, the color of the card directed the weight to be first diminished and then increased, the operator had the differential weight already on the pan of the balance before the pressure was brought to bear on the finger, and made the reverse changes at the command of the subject. The subject then stated his judgment and also his degree of confidence, whereupon the total pressure was at once removed by the cam, and the card that had been used to direct the change was placed face down or face up according as the answer was right or wrong, and with corner indicating the degree of confidence in a determinate position. By means of these trifling devices the important object of rapidity was secured, and any possible psychological guessing of what change the operator was likely to select was avoided. A slight disadvantage in this mode of proceeding arises from the long runs of one particular kind of change, which would occasionally be produced by chance and would tend to confuse the mind of the subject. But it seems clear that this disadvantage was less than that which would have been occasioned by his knowing that there would be no such long runs if any means had been taken to prevent them. At the end of each set the results were of course entered into a book.[6]
The following tables show the results of the observations for each day:
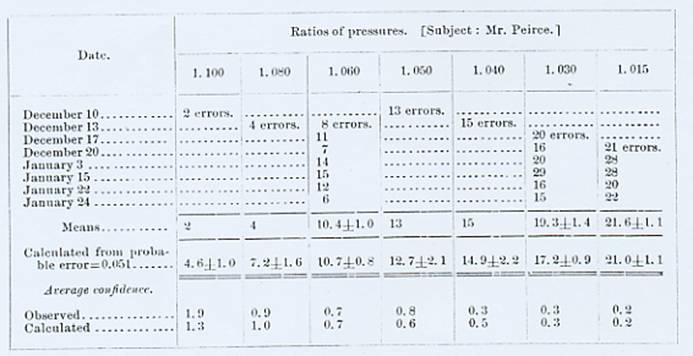
The numbers in the columns show the number of errors in fifty experiments. With the average number of errors in a set of fifty we compare the theoretical value of this average as calculated by the method of least squares. The number .051 thus obtained in this case best satisfies the mean number of errors. The numbers affixed with a sign denote, in the upper row the observed (a posteriori) probable error of the mean value as given, in the lower row the calculated (a priori) probable error. The last two lines give the average confidence observed and calculated with each variation of the ratios of pressure. It will be seen that the correspondence between the real and theoretical numbers is close, and closest when the number of sets is large. The probable errors also closely correspond, the observed being, as is natural, slightly larger than the calculated probable errors.[p. 81]
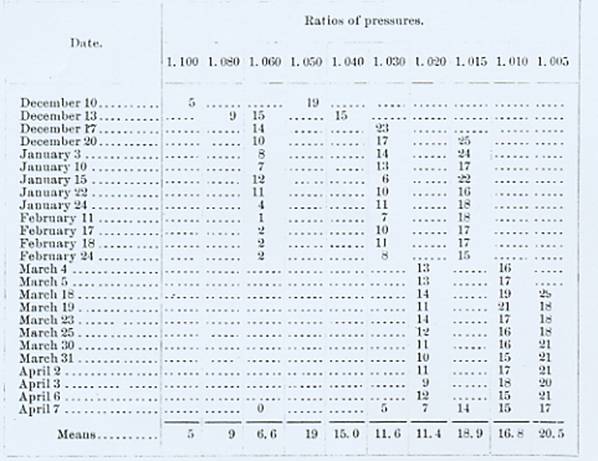
The following is a similar table for Mr. Jastrow as subject:It would obviously be unfair to compare these numbers with any set of theoretical numbers, since the probable error is on the decrease throughout, owing to effects of practice, etc. For various reasons we can conveniently group these experiments into four groups. The first will include the experiments from December 10 to January 22, inclusive; the second from January 24 to February 24, inclusive; the third from March 4 to March 25, inclusive; the fourth from March 30 to the end of the work. The mean results for the different groups are exhibited in the following tables:[p. 82]
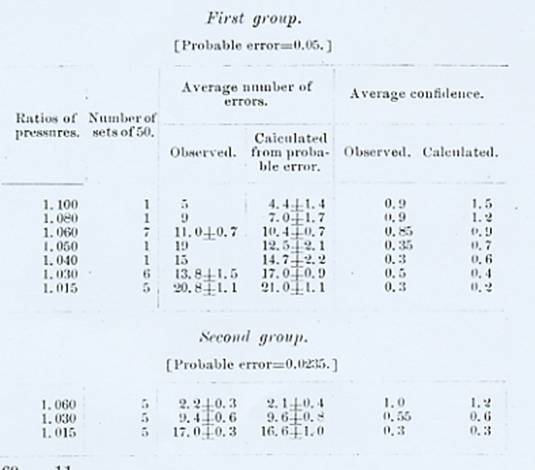
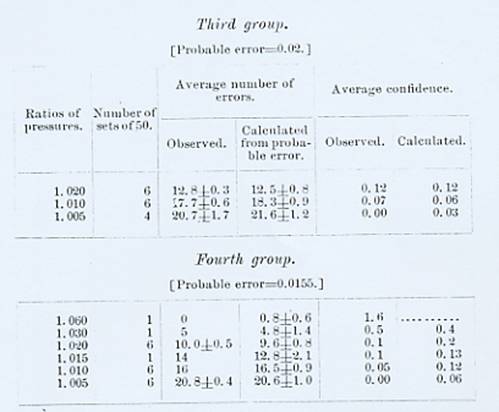
The tables show that the numbers of errors follow, as far as we can
conveniently trace them, the numbers assigned by the probability curve,[7] and therefore destroy all presumption in favor of an Unterschiedsschwelle.
The introduction and retention of this false notion can only confuse thought,
while the conception of the mathematician must exercise a favorable influence
on psychological experimentation.[8]
The quantity which we have called the degree of confidence was probably the secondary sensation of a difference between the primary sensations compared. The evidence of our experiments [p. 83] seems clearly to be that this sensation has no Schwelle, and vanishes only when the difference to which it refers vanishes. At the same time we found the subject often overlooked this element of his field of sensation, although his attention was directed with a certain strength toward it, so that he marked his confidence as zero. This happened in cases where the judgments were so much affected by the difference of pressures as to be correct three times out of five. The general fact has highly important practical bearings, since it gives new reason for believing that we gather what is passing in one another's minds in large measure from sensations so faint that we are not fairly aware of having them, and can give no account of how we reach our conclusions about such matters. The insight of females as well as certain "telepathic" phenomena may be explained in this way. Such faint sensations ought to be fully studied by the psychologist and assiduously cultivated by every man.
Notes
[1] Elemente der Psychophysik, I, p. 242.
[2] The rule for finding this ratio is as follows: Divide the logarithm of the ratio of excitations by the probable error and multiply the quotient by 0.477. Call this product t. Enter it in the table of the integral θt, given in most works on probabilities; θt is the proportion of cases in which the error will be less than the difference between the given excitations. In all these cases, of course, we shall answer correctly, and also by chance in one-half of the remaining cases. The proportion of erroneous answers is therefore (1-θt)/2. In the following table the first column gives the quotient of the logarithm of the ratio of excitation, divided by the probable error, and the second column shows the proportion of erroneous judgments:To guess the correct card out of a pack of fifty-two once in eleven times it would be necessary to have a sensation amounting to 0.37 of the probable error. This would be a sensation of which we should probably never become aware, as will appear below.

[3] The number of errors, when an increase of weight was followed by a
decrease, was slightly less than when the first change was a decrease of
pressure.
[4]
The result of our observations on the confidence connected with the judgments
is as follows: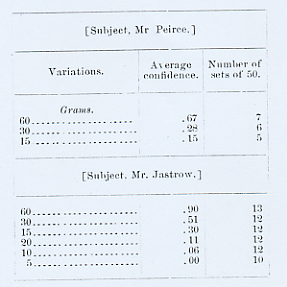
In 1,125 experiments (subject, Mr. Peirce) -- variations 15, 30, and 60 grams
-- there occurred confidence of 3, 35 times (3 per cent.); of 2, 102 times (9
per cent.); of 1, 282 times (25 per cent.); of 0, 706 times (63 per cent.). In
these experiments there were 332 (29 per cent.) errors committed, of which 1
(0.3 per cent.) was made in connection with a confidence 3; 10 (3 per cent.)
with a confidence 2; 51 (15 per cent.) with a confidence 1; 270 (81 per cent.)
with a confidence 0. From which we find that in connection with a confidence of
3 there occurred 1 error in 35 cases (3 per cent.); with a confidence of 2, 10
errors in 102 cases (10 per cent.); with a confidence of 1, 51 errors in 282
cases (18 per cent.); with a confidence of 0, 270 errors in 706 cases (38 per
cent.).
In 1,975 experiments (subject, Mr. Jastrow) -- variations 15, 30, and 60 grams -- there occurred confidence of 3, 62 times (3 per cent.); of 2, 196 times (10 per cent.); of 1, 594 times (30 per cent.); of 0, 1,123 times (57 per cent.). In these experiments there were 451 (23 per cent.) errors committed, of which 2 (0.4 per cent.) were made in connection with a confidence of 3; 12 (3 per cent.) with a confidence of 2; 97 (22 per cent.) with a confidence of 1; 340 (75 per cent.) with a confidence of 0. Again, in connection with a confidence of 3, errors occurred twice in 62 cases (3 per cent.); with a confidence of 2, 12 times in 196 cases (6 per cent.); with a confidence of 1, 97 times in 504 cases (16 per cent.); with a confidence of 0, 340 times in 1,123 cases (30 per cent.).
In 1,675 experiments (subject, Mr. Jastrow) -- variations 5, 10, and 20 grams -- there occurred confidences of 3, none; of 2, none; of 1, 115 times (7 per cent.); of 0, 1,560 times (93 per cent.). In these experiments there were 538 (32 per cent.) errors committed, of which 16 (3 per cent.) occurred in connection with a confidence of 1; 522 (97 per cent.) with a confidence of 0. Again, in connection with a confidence of 1, errors occurred 16 times in 115 cases (14 per cent.); with a confidence of 0, 522 times in 1,560 cases (34 per cent.).
[5] At first a short pause was made in the set of 25, at the option of the subject; later this was dispensed with.
[6] In the experiments of December, 1883, and January, 1884, the method as above described was not fully perfected, the most important fault being that the total weight instead of being removed and replaced by a mechanical device, was taken off by the operator pressing with his finger upon the beam of the balance.


[7] In the tables of the third and fourth groups, there is a markeddivergence
between the a priori and a posteriori probable error, for theaverage number of
errors in 50, making the observed probable error toosmall. This can only be
partly accounted for by the fact that thesubject formed the unconscious habit
of retaining the number of eachkind of experiment in a set and answering
according to that knowledge.In point of fact the plus errors and minus errors
separately do notexhibit the singular uniformity of their sums, for which we
are quiteunable to account. Thus in the fourth group we have:[8]
The conclusions of this paper are strengthened by the results of a series of
experiments on the color sense, made with the use of a photometer by Mr.
Jastrow. The object was to determine the number of errors of a given magnitude,
and compare the numbers thus ascertained with the theoretical numbers given by
the probability curve. A thousand experiments were made. Dividing the magnitude
of the errors from 0 to the largest error, made into 5 parts, the number of
errors, as observed and calculated, that occur in each part are as follows: These
numbers would be in closer accordance if the probable error were the same
throughout, as it is not owing to the effects of practice, etc. Moreover, the
experiments were made on different colors -- 300 on white and 100 each on
yellow, blue, dove, pink, green, orange, and brown. These experiments were not
continuous.