Classics in the History of Psychology

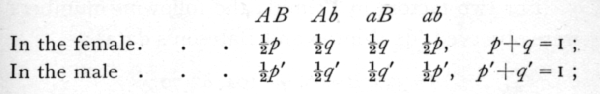
An internet resource developed by
Christopher D. Green
York University, Toronto, Ontario
ISSN 1492-3173

(Return to index)

STATISTICAL METHODS FOR RESEARCH WORKERS

INTRODUCTORY

The science of statistics is essentially a branch of Applied Mathematics and may be regarded as mathematics applied to observational data. As in other mathematical studies the same formula is equally relevant to widely different groups of subject matter. Consequently the unity of the different applications has usually been overlooked, the more naturally because the development of the underlying mathematical theory has been much neglected. We shall therefore consider the subject matter of statistics under three different aspects, and then show in more mathematical language that the same types of problems arise in every case. Statistics may be regarded as (i.) the study of populations, (ii.) as the study of variation, (iii.) as the study of methods of the reduction of data.

The original meaning of the word "statistics" [p. 2] suggests that it was the study of populations of human beings living in political union. The methods developed, however, have nothing to do with the political unity of the group, and are not confined to populations of men or of social insects. Indeed, since no observational record can completely specify a human being, the populations studied are to some extent abstractions. If we have records of the stature of 10,000 recruits, it is rather the population of statures than the population of recruits that is open to study. Nevertheless, in a real sense, statistics is the study of populations, or aggregates of individuals, rather than of individuals. Scientific theories which involve the properties of large aggregates of individuals, and not necessarily the properties of the individuals themselves, such as the Kinetic Theory of Gases, the Theory of Natural Selection, or the chemical Theory of Mass Action, are essentially statistical arguments; and are liable to misinterpretation as soon as the statistical nature of the argument is lost sight of. Statistical. methods are essential to social studies, and it is principally by the aid of such methods that these studies may be raised to the rank of sciences. This particular dependence of social studies upon statistical methods has led to the painful misapprehension that statistics is to be regarded as a branch of economics, whereas in truth economists have much to learn from their scientific contemporaries, not only in general scientific method, but in particular in statistical practice.

The idea of a population is to be applied not only [p. 3] to living, or even material, individuals. If an observation, such as a simple measurement, be repeated a number of times, the aggregate of the results is a population of measurements. Such populations are the particular field of study of the Theory of Errors, one of the oldest and most fruitful lines of statistical investigation. Just as a single observation may be regarded as an individual, and its repetition as generating a population, so the entire result of an extensive experiment may be regarded as but one of a population of such experiments. The salutary habit of repeating important experiments, or of carrying out original observations in replicate, shows a tacit appreciation of the fact that the object of our study is not the individual result, but the population of possibilities of which we do our best to make our experiments representative. The calculation of means and probable errors shows a deliberate attempt to find out something about that population.

The conception of statistics as the study of variation is the natural outcome of viewing the subject as the study of populations; for a population of individuals in all respects identical is completely described by a description of any one individual, together with the number in the group, The populations which are the object of statistical study always display variation in one or more respects. To speak of statistics as the study of variation also serves to emphasise the contrast between the aims of modern statisticians and those of their predecessors. For, until comparatively recent times, the vast majority [p. 4] of workers in this field appear to have had no other aim than to ascertain aggregate, or average, values.

The variation itself was not an object of study, but was recognised rather as a troublesome circumstance which detracted from the value of the average. The error curve of the mean of a normal sample has been familiar for a century, but that of the standard deviation has scarcely been securely established for a decade. Yet, from the modern point of view, the study of the causes of variation of any variable phenomenon, from the yield of wheat to the intellect of man, should be begun by the examination and measurement of the variation which presents itself.

The study of variation leads immediately to the concept of a frequency distribution. Frequency distributions are of various kinds, according as the number of classes in which the population is distributed is finite or infinite, and also according as the intervals which separate the classes are finite or infinitesimal. In the simplest possible case, in which there are only two classes, such as male and female births, the distribution is simply specified by the proportion in which these occur, as for example by the statement that 51 per cent of the births are of males and 49 per cent of females. In other cases the variation may be discontinuous, but the number of classes indefinite, as with the number of children born to different married couples; the frequency distribution would then show the frequency with which 0, 1, 2 ... children were recorded, the number of classes being sufficient to include the largest family in the record. [p. 5] The variable quantity, such as the number of children, is called the variate, and the frequency distribution specifies how frequently the variate takes each of its possible values. In the third group of cases, the variate, such as human stature, may take any intermediate value within its range of variation; the variate is then said to vary continuously, and the frequency distribution may be expressed by stating, as a mathematical function of the variate, either (i.) the proportion of the population for which the variate is less than any given value, or (ii.) by the mathematical device of differentiating this function, the (infinitesimal) proportion of the population for which the variate falls within any infinitesimal element of its range.

The idea of a frequency distribution is applicable either to populations which are finite in number, or to infinite populations, but it is more usefully and more simply applied to the latter. A finite population can only be divided in certain limited ratios, and cannot in any case exhibit continuous variation. Moreover, in most cases only an infinite population can exhibit accurately, and in their true proportion, the whole of the possibilities arising from the causes actually at work, and which we wish to study. The actual observations can only be a sample of such possibilities. With an infinite population the frequency distribution specifies the fractions of the populations assigned to the several classes; we may have (i.) a finite number of fractions adding up to unity as in the Mendelian frequency distributions, or (ii.) an infinite series of finite fractions adding up to unity, or (iii.) a mathematical [p. 6] function expressing the fraction of the total in each of the infinitesimal elements in which the range of the variate may be divided. The last possibility may be represented by a frequency curve; the values of the variate are set out along a horizontal axis, the fraction of the total population, within any limits of the variate, being represented by the area of the curve standing on the corresponding length of the axis. It should be noted that the familiar concept of the frequency curve is only applicable to infinite populations with continuous variates.

The study of variation has led not merely to measurement of the amount of variation present, but to the study of the qualitative problems of the type, or form, of the variation. Especially important is the study of the simultaneous variation of two or more variates. This study, arising principally out of the work of Galton and Pearson, is generally known in English under the name of Correlation, but by some continental writers as Covariation.

The third aspect under which we shall regard the scope of statistics is introduced by the practical need to reduce the bulk of any given body of data. Any investigator who has carried out methodical and extensive observations will probably be familiar with the oppressive necessity of reducing his results to a more convenient bulk. No human mind is capable of grasping in its entirety the meaning of any considerable quantity of numerical data. We want to be able to express all the relevant information contained in the mass by means of comparatively few numerical [p. 7] values. This is a purely practical need which the science of statistics is able to some extent to meet. In some cases at any rate it is possible to give the whole of the relevant information by means of one or a few values. In all cases, perhaps, it is possible to reduce to a simple numerical form the main issues which the investigator has in view, in so far as the data are competent to throw light on such issues. The number of independent facts supplied by the data is usually far greater than the number of facts sought, and in consequence much of the information supplied by any body of actual data is irrelevant. It is the object of the statistical processes employed in the reduction of data to exclude this irrelevant information, and to isolate the whole of the relevant information contained in the data.

The discrimination between the irrelevant and the relevant information is performed as follows. Even in the simplest cases the values (or sets of values) before us are interpreted as a random sample of a hypothetical infinite population of such values as might have arisen in the same circumstances. The distribution of this population will be capable of some kind of mathematical specification, involving a certain number, usually few, of parameters, or "constants" entering into the mathematical formula. These parameters are the characters of the population. If we could know the exact specification of the population, we should know all (and more than) any sample from [p. 8] the population could tell us. We cannot in fact know the specification exactly, but we can make estimates of the unknown parameters, which will be more or less inexact. These estimates, which are termed statistics, are of course calculated from the observations. If we can find a mathematical form for the population which adequately represents the data, and then calculate from the data the best possible estimates of the required parameters, then it would seem that there is little, or nothing, more that the data can tell us; we shall have extracted from it all the available relevant information.

The value of such estimates as we can make is enormously increased if we can calculate the magnitude and nature of the errors to which they are subject. If we can rely upon the specification adopted, this presents the purely mathematical problem of deducing from the nature of the population what will be the behaviour of each of the possible statistics which can be calculated. This type of problem, with which until recent years comparatively little progress had been made, is the basis of the tests of significance by which we can examine whether or not the data are in harmony with any suggested hypothesis. In particular, it is necessary to test the adequacy of the hypothetical specification of the population upon which the method of reduction was based.

The problems which arise in the reduction of data may thus conveniently be divided into three types:

(i.) Problems of Specification, which arise in the choice of the mathematical form of the population. [p. 9]

(ii.) Problems of Estimation, which involve the choice of method of calculating, from our sample, statistics fit to estimate the unknown parameters of the population.

(iii.) Problems of Distribution, which include the mathematical deduction of the exact nature of the distribution in random samples of our estimates of the parameters, and of other statistics designed to test the validity of our specification (tests of Goodness of Fit).

The statistical examination of a body of data is thus logically similar to the general alternation of inductive and deductive methods throughout the sciences. A hypothesis is conceived and defined with necessary exactitude; its consequences are deduced by a deductive argument; these consequences are compared with the available observations; if these are completely in accord with the deductions, the hypothesis may stand at any rate until fresh observations are available.

The deduction of inferences respecting samples, from assumptions respecting the populations from which they are drawn, shows us the position in Statistics of the Theory of Probability. For a given population we may calculate the probability with which any given sample will occur, and if we can solve the purely mathematical problem presented, we can calculate the probability of occurrence of any given statistic calculated from such a sample. The Problems of Distribution may in fact be regarded as applications and extensions of the theory of probability. [p. 10] Three of the distributions with which we shall be concerned, Bernoulli's binomial distribution, Laplace's normal distribution, and Poisson's series, were developed by writers on probability. For many years, extending over a century and a half, attempts were made to extend the domain of the idea of probability to the deduction of inferences respecting populations from assumptions (or observations) respecting samples. Such inferences are usually distinguished under the heading of Inverse Probability, and have at times gained wide acceptance. This is not the place to enter into the subtleties of a prolonged controversy; it will be sufficient in this general outline of the scope of Statistical Science to express my personal conviction, which I have sustained elsewhere, that the theory of inverse probability is founded upon an error, and must be wholly rejected. Inferences respecting populations, from which known samples have been drawn, cannot be expressed in terms of probability, except in the trivial case when the population is itself a sample of a super-population the specification of which is known with accuracy.

This is not to say that we cannot draw, from knowledge of a sample, inferences respecting the population from which the sample was drawn, but that the mathematical concept of probability is inadequate to express our mental confidence or diffidence in making such inferences, and that the mathematical quantity which appears to be appropriate for measuring our order of preference among different possible populations does not in fact obey the laws of probability. [p. 11] To distinguish it from probability, I have used the term "Likelihood" to designate this quantity; since both the words "likelihood" and "probability" are loosely used in common speech to cover both kinds of relationship.

The solutions of problems of distribution (which may be regarded as purely deductive problems in the theory of probability) not only enable us to make critical tests of the significance of statistical results, and of the adequacy of the hypothetical distribution upon which our methods of numerical deduction are based, but afford some guidance in the choice of appropriate statistics for purposes of estimation. Such statistics may be divided into classes according to the behaviour of their distributions in large samples.

If we calculate a statistic, such, for example, as the mean, from a very large sample, we are accustomed to ascribe to it great accuracy; and indeed it would usually, but not always, be true, that if a number of such statistics could be obtained and compared, the discrepancies between them would grow less and less, as the samples from which they are drawn are made larger and larger. In fact, as the samples are made larger without limit, the statistic will usually tend to some fixed value characteristic of the population, and, therefore, expressible in terms of the parameters of the population. If, therefore, such a statistic is to be used to estimate these parameters, there is only one parametric function to which it can properly be equated. [p. 12] If it be equated to some other parametric function, we shall be using a statistic which even from an infinite sample does not give the correct value; it tends indeed to a fixed value, but to a value which is erroneous from the point of view with which it was used. Such statistics are termed Inconsistent Statistics; except when the error is extremely minute, as in the use of Sheppard's corrections, inconsistent statistics should be regarded as outside the pale of decent usage.

Consistent statistics, on the other hand, all tend more and more nearly to give the correct values, as the sample is more and more increased; at any rate, if they tend to any fixed value it is not to an incorrect one. In the simplest cases, with which we shall be concerned, they not only tend to give the correct value, but the errors, for samples of a given size, tend to be distributed in a well-known distribution (of which more in Chap. III.) known as the. Normal Law of Frequency of Error, or more simply as the normal distribution. The liability to error may, in such cases, be expressed by calculating the mean value of the squares of these errors, a value which is known as the variance; and in the class of cases with which we are concerned, the variance falls off with increasing samples, in inverse proportion to the number in the sample.

Now, for the purpose of estimating any parameter, it is usually possible to invent any number of statistics which shall be consistent in the sense defined above, and each of which has in large samples a variance falling off inversely with the size of the sample. But [p. 13] for large samples of a fixed size, the variance of these different statistics will generally be different. Consequently a special importance belongs to a smaller group of statistics, the error distributions of which tend to the normal distribution, as the sample is increased, with the least possible variance. We may thus separate off from the general body of consistent statistics a group of especial value, and these are known as efficient statistics.

The reason for this term may be made apparent by an example. If from a large sample of (say) 1000 observations we calculate an efficient statistic, A, and a second consistent statistic, B, having twice the variance of A, then B will be a valid estimate of the required parameter, but one definitely inferior to A in its accuracy. Using the statistic B, a sample of 2000 values would be required to obtain as good an estimate as is obtained by using the statistic A from a sample of 1000 values. We may say, in this sense, that the statistic B makes use of 50 per cent of the relevant information available in the observations; or, briefly, that its efficiency is 50 per cent. The term "efficient" in its absolute sense is reserved for statistics the efficiency of which is 100 per cent.

Statistics having efficiency less than 100 per cent may be legitimately used for many purposes. It is conceivable, for example, that it might in some cases be laborious to increase the number of observations than to apply a more elaborate method of calculation the results. It may often happen that an inefficient statistic is accurate enough to answer the particular [p. 14] questions at issue. There is, however, one limitation to the legitimate use of inefficient statistics which should be noted in advance. If we are to make accurate tests of goodness of fit, the methods of fitting employed must not introduce errors of fitting comparable to the errors of random sampling; when this requirement is investigated, it appears that when tests of goodness of fit are required, the statistics employed in fitting must be not only consistent, but must be of 100 per cent efficiency. This is a very serious limitation to the use of inefficient statistics, since. in the examination of any body of data it is desirable to be able at any time to test the validity of one or more of the provisional assumptions which have been made.

Numerous examples of the calculation of statistics will be given in the following chapters, and in these illustrations of method efficient statistics have been chosen. The discovery of efficient statistics in new types of problem may require some mathematical investigation. The investigations of the author have led him to the conclusion that an efficient statistic can in all cases be found by the Method of Maximum Likelihood; that is, by choosing statistics so that the estimated population should be that for which the likelihood is greatest. In view of the mathematical difficulty of some of the problems which arise it is also useful to know that approximations to the maximum likelihood solution are also in most cases efficient statistics. A simple example of the application of the method of maximum likelihood to a genetical problem is given at the end of this chapter. [p. 15]

For practical purposes it is not generally necessary to press refinement of methods further than the stipulation that the statistics used should be efficient. With large samples it may be shown that all efficient statistics tend to equivalence, so that little inconvenience arises from diversity of practice. There is, however, one class of statistics, including some of the most frequently recurring examples, which is of theoretical interest for possessing the remarkable property that, even in small samples, a statistic of this class alone includes the whole of the relevant information which the observations contain. Such statistics are distinguished by the term sufficient, and, in the use of small samples, sufficient statistics, when they exist, are definitely superior to other efficient statistics. Examples of sufficient statistics are the arithmetic mean of samples from the normal distribution, or from the Poisson Series; it is the fact of providing sufficient statistics for these two important types of distribution which gives to the arithmetic mean its theoretical importance. The method of maximum likelihood leads to these sufficient statistics where they exist.

While diversity of practice within the limits of efficient statistics will not with large samples lead to inconsistencies, it is, of course, of importance in all cases to distinguish clearly the parameter of the population, of which it is desired to estimate the value, from the actual statistic employed as an estimate of its value; and to inform the reader by which of the considerable variety of processes which exist for the purpose the estimate was actually obtained. [p. 16]

The prime object of this book is to put into the hands of research workers, and especially of biologists, the means of applying statistical tests accurately to numerical data accumulated in their own laboratories or available in the literature. Such tests are the result of solutions of problems of distribution, most of which are but recent additions to our knowledge and have so far only appeared in specialised mathematical papers. The mathematical complexity of these problems has made it seem undesirable to do more than (i.) to indicate the kind of problem in question, (ii.) to give numerical -illustrations by which the whole process may be checked, (iii.) to provide numerical tables by means of which the tests may be made without the evaluation of complicated algebraical expressions .

It would have been impossible to give methods suitable for the great variety of kinds of tests which are required but for the unforeseen circumstances that each mathematical solution appears again and again in questions which at first sight appeared to be quite distinct. For example, Pearson's solution in 1900 of the distribution of c² is in reality equivalent to the distribution of the variance as estimated from normal samples, of which the solution was not given until 1908, and then quite tentatively, and without complete mathematical proof, by "Student." The same distribution was found by the author for the index of dispersion derived from small samples from a Poisson [p. 17] Series. What is even more remarkable is that, though Pearson's paper of 1900 contained a serious error, which vitiated most of the tests of goodness of fit made by this method until 1921, yet the correction of this error leaves the form of the distribution unchanged, and only requires that some few units should be deducted from one of the variables with which the table of c² is entered.

It is equally fortunate that the distribution of t, first established by "Student" in 1908, in his study of the probable error of the mean, should be applicable, not only to the case there treated, but to the more complex, but even more frequently needed problem of the comparison of two mean values. It further provides an exact solution of the sampling errors of the enormously wide class of statistics known as regression coefficients.

In studying the exact theoretical distributions in a number of other problems, such as those presented by intraclass correlations, the goodness of fit of regression lines, the correlation ratio, and the multiple correlation coefficient, the author has been led repeatedly to a third distribution, which may be called the distribution of z, and which is intimately related to, and 'indeed a natural extension of, the distributions found by Pearson and "Student." It has thus been possible to classify the necessary distributions, covering a very great variety of cases, under these three main groups; and, what is equally important, to make some provision for the need of numerical values by means of a few tables only. [p. 18]

The book has been arranged so that the student may make acquaintance with these three main distributions in a logical order, and proceeding from more simple to more complex cases. Methods developed in later chapters are frequently seen to be generalisations of simpler methods developed previously. Studying the work methodically as a connected treatise, the student will, it is hoped, not miss the fundamental unity of treatment under which such very varied material has been brought together; and will prepare himself to deal competently and with exactitude with the many analogous problems, which cannot be individually exemplified. On the other hand, it is recognised that many will wish to use the book for laboratory reference, and not as a connected course of study. This use would seem desirable only if the reader will be at the pains to work through, in all numerical detail, one or more of the appropriate examples, so as to assure himself, not only that his data are appropriate for a parallel treatment, but that he has obtained some critical grasp of the meaning to be attached to the processes and results.

It is necessary to anticipate one criticism, namely, that in an elementary book, without mathematical proofs, and designed for readers without special mathematical training, so much has been included which from the teacher's point of view is advanced; and indeed much that has not previously appeared in print. By way of apology the author would like to put forward the following considerations.

(1) For non - mathematical readers, numerical [p. 19] tables are in any case necessary; accurate tables are no more difficult to use, though more laborious to calculate, than inaccurate tables embodying the current approximations.

(2) The process of calculating a probable error from one of the established formulæ gives no real insight into the random sampling distribution, and can only supply a test of significance by the aid of a table of deviations of the normal curve, and on the assumption that the distribution is in fact very nearly normal. Whether this procedure should, or should not, be used must be decided, not by the mathematical attainments of the investigator, but by discovering whether it will or will not give a sufficiently accurate answer. The fact that such a process has been used successfully by eminent mathematicians in analysing very extensive and important material does not imply that it is sufficiently accurate for the laboratory worker anxious to draw correct conclusions from a small group of perhaps preliminary observations.

(3) The exact distributions, with the use of which this book is chiefly concerned, have been in fact developed in response to the practical problems arising in biological and agricultural research; this is true not only of the author's own contribution to the subject, but from the beginning of the critical examination of statistical distributions in "Student's " paper of 1908.

The greater part of the book is occupied by numerical examples; and these perhaps could with advantage have been increased in number. In choosing them it has appeared to the author a hopeless task [p. 20] to attempt to exemplify the great variety of subject matter to which these processes may be usefully applied. There are no examples from astronomical statistics, in which important work has been done in recent years, few from social studies, and the biological applications are scattered unsystematically. The examples have rather been chosen each to exemplify a particular process, and seldom on account of the importance of the data used, or even of similar examinations of analogous data. By a study of the processes exemplified, the student should be able to ascertain to what questions, in his own material, such processes are able to give a definite answer; and, equally important, what further observations would be necessary to settle other outstanding questions. In conformity with the purpose of the examples the reader should remember that they do not pretend to be critical examinations of general scientific questions, which would require the examination of much more extended data, and of other evidence, but are solely concerned with the evidence of the particular batch of data presented.

The tables of distributions supplied at the ends of several chapters form a part essential to the use of the book.

TABLES I. AND II.-The importance of the normal distribution has been recognised at least from the time of Laplace. (The formula has even been traced back to a little-known work by De Moivre of 1733) Numerous tables have given in one form or another the relation between the deviation, and the probability of a greater deviation. Important sources for these values are

The very various forms in which this relation has been tabulated adds considerably to the labour of practical applications. The form which we have adopted for this, and for the other tables, has been used for the normal distribution by

both of which are valuable tables, on a more extensive scale than Table I. In Table II. we have given the normal deviations corresponding to very high odds. It should be remembered that even slight departures from the normal distribution will render these very small probabilities relatively very inaccurate, and that we seldom can be certain, in any particular case, that these high odds will be accurate. The table illustrates the general fact that the significance in the normal distribution of deviations exceeding four times the standard deviation is extremely pronounced.

TABLE III.; table of c². -- Tables of the value of P for different values of c² and n', were given by

Table III. gives the values of c² for different values of P and n, in a form designed for rapid laboratory use, and with a view to covering in sufficient detail the range of values actually occurring in practice. For higher values of n the test is supplemented by an easily calculated approximate test.

TABLE IV.; table of t. -- Tables of the same distribution as that of t have been given by

"Student" gives the value of (1-½P) for different values of z (=t/[sqrt]n in our notation) and n (=n+1 in our notation). As in the case of the table of c², the very much extended application of this distribution has led to a reinterpretation of the meaning of n to cover a wider class of cases. Extended tables giving the values of P for different values of t are in preparation by the same author. For the purposes of the present book we require the values of t corresponding to given values of P and n.

TABLE V. A gives the values of the correlation coefficient for different levels of significance, according to the extent of the sample upon which the value is based. From this table the reader may see at a glance whether or not any correlation obtained may be regarded as significant, for samples up to 100 pairs of observations. [p. 23]

TABLE V. B gives the values of the well-known mathematical function, the hyperbolic tangent, which we have introduced in the calculation of sampling errors of the correlation coefficient. The function is simply related to the logarithmic and exponential functions, and may be found quite easily by such a convenient table of natural logarithms as is given in

while the hyperbolic tangent and its inverse appear in

A table of natural logarithms is in other ways a necessary supplement in using this book, as in other laboratory calculations. Tables of the inverse hyperbolic tangent for correlational work have been previously given by

TABLE VI.; table of z. -- Tests involving the use of z, including as special cases the use of c² and of t, are so widespread, that it is probable that a more extended table of this function will be necessary. The exploration of this function is of such recent date, and the construction of a table of triple entry is such a laborious task, that all that can be offered at present is the small table corresponding to the important region, P= .05 It is probable, indeed, that if supplemented by a similar table for P=.01, all ordinary requirements would be met, although to avoid the labour of interpolation much larger tables for these two values would be needed.

At present I can only beg the reader's indulgence [p. 24] for the inadequacy of the present table, pleading in my defence that, on ground so recently won as is that occupied by the greater part of this book, the full facilities and conveniences which many workers can gradually accumulate cannot yet be expected.

6. The following example exhibits in a relatively simple case the application of the method of maximum likelihood to discover a statistic capable of giving an efficient estimate of an unknown parameter. Since this procedure belongs rather to the advanced mathematical treatment of theoretical statistics, it may be noted that to master it is not a necessary preliminary to understanding the practical methods developed in the rest of the book. Students, however, who wish to apply the fundamental principles mentioned in this introductory chapter to new types of data, may perhaps be glad of an example of the general procedure.

Ex. 1. The derivation of an efficient statistic by means of the method of maximum likelihood. -- Animals or plants heterozygous for two linked factors showing complete dominance are self fertilised ; if all four types are equally viable, how should the extent of linkage be estimated from the numerical proportions of the four types of offspring?

If the allelomorphs of the first factor are A and a, and of the second factor B and b, the four types of gametes AB, Ab, aB and ab will be produced by the males and females in proportions depending on the linkage of the factors, subject to the condition that the allelomorphs of each factor occur equally frequently. [p. 25] The proportions will the two sexes; suppose the proportions to be

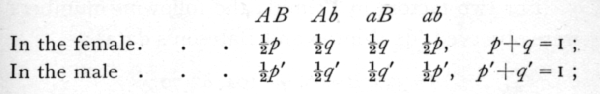
then, if the two dominant genes are derived from the same parent, q, q' will be the cross-over ratios, if from different parents the cross-over ratios will be p, p'.

By taking all possible combinations of the gametes, it appears that the four types of offspring will occur in the proportions

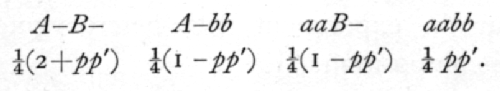
The effect of linkage is wholly expressed by the quantity pp', and from a sample of observations giving observed frequencies a, b, g, d, we require to obtain an estimate of the value of pp'. The rule for applying the method of maximum likelihood is to multiply each observed frequency by the logarithm of the corresponding theoretical frequency, and to find the value of the unknown quantity which makes the total of these products a maximum. Writing x for pp',

a log (2+x) + (b+g) log (1-x) + d log x

is to be made a maximum; by a well-known application of the differential calculus, this requires that

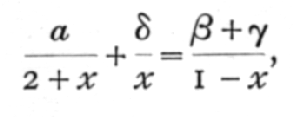
which leads to the quadratic equation for x,

(a+b+g+d)x² - (a-2b-2g-d)x - 2d = 0, [p. 26]

the positive solution of which is the most likely value for pp', as judged from the data.

For two factors in Primula the following numbers were observed (de Winton and Bateson's data):

a=396, b=99, g=104, d=70;

the quadratic for x is

669x² + 80x - 140 = 0,

of which the positive solution is x = .4016. To obtain the cross-over values in the two sexes separately, using self-fertilisation only, it would of course be necessary to repeat the experiment with heterozygotes of the opposite composition.

The numbers expected, on the supposition that pp' = 4016, are :