
Classics in the History of Psychology
An internet resource developed by
Christopher D. Green
York University, Toronto, Ontario
(Return to index)
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER IX
RETENTION AS A FUNCTION OF THE ORDER OF
SUCCESSION OF THE MEMBERS OF THE SERIES
"How odd are the connections
Of human thoughts which jostle in their flight."
Section 35. Association according to Temporal Sequence and its Explanation
I shall now discuss a group of investigations made for the purpose of finding out the conditions of association. The results of these investigations are, it seems to me, theoretically of especial interest.
The non-voluntary re-emergence of mental images out of the darkness of memory into the light of consciousness takes place, as has already been mentioned, not at random and accidentally, but in certain regular forms in accordance with the so-called laws of association. General knowledge concerning these laws is as old as psychology itself, but on the other hand a more precise formulation of them has remained -- characteristically enough -- a matter of dispute up to the very present. Every new presentation starts out with a reinterpretation of the contents of a few lines from Aristotle, and according to the condition of our knowledge it is necessary so to do.
Of these "Laws," now -- if, in accordance with usage and it is to be hoped in anticipation of the future, the use of so lofty a term is permitted in connection with formulae of so vague a character -- of these laws, I say, there is one which has never been disputed or doubted. It is usually formulated as follows:
Ideas which have been developed simultaneously or in immediate succession in the same mind mutually reproduce each other, and do this with greater ease in the direction of the original succession and with a certainty proportional to the frequency with which they were together.
This form of non-voluntary reproduction is one of the best verified and most abundantly established facts in the whole realm of mental events. It permeates inseparably every form of reproduction, even the so-called voluntary form. The function of the conscious will, for example, in all the numerous reproductions of the syllable-series which we have come to know, is limited to the general purpose of reproduction and to laying hold of the first member of the series. The remaining members follow automatically, so to speak, and thereby fulfill the law that things which have occurred together in a given series are reproduced in the same order.
However, the mere recognition of these evident facts has naturally not been satisfying and the attempt has been made to penetrate into the inner mechanism of which they are the result. If for a moment we try to follow up this speculation concerning the Why, before we have gone more than two steps we are lost in obscurities and bump up against the limits of our knowledge of the How.
It is customary to appeal for the explanation of this form of association to the nature of the soul. Mental events, it is said, are not passive happenings but the acts of a subject. What is more natural than that this unitary being should bind together in a definite way the contents of his acts, themselves also unified? Whatever is experienced simultaneously or in immediate succession is conceived in one act of consciousness and by that very means its elements are united and the unison is naturally stronger in proportion to the number of times they are entwined by this bond of conscious unity. Whenever, now, by any chance one part only of such a related complex is revived, what else can it do than to attract to itself the remaining parts?
But this conception does not explain as much as it was intended to do. For the remaining parts of the complex are not merely drawn forth but they respond to the pull in an altogether definite direction. If the partial contents are united simply by the fact of their membership in a single conscious act and accordingly all in a similar fashion, how does it come about that a sequence of partial contents returns in precisely the same order and not in any chance combination? In order to make this intelligible, one can proceed in two ways.
In the first place it can be said that the connection of the things present simultaneously in a single conscious act is made from each member to its immediate successor but not to members further distant. This connection is in some way inhibited by the presence of intermediate members, but not by the interposition of pauses, provided that the beginning and end of the pause can be grasped in one act of consciousness. Thereby return is made to the facts, but the advantage which the whole plausible appeal to the unitary act of consciousness offered is silently abandoned. For, however much contention there may be over the number of ideas which a single conscious act may comprehend, it is quite certain that, if not always, at least in most cases, we include more than two members of a series in any one conscious act. If use is made of one feature of the explanation, the characteristic of unity, as a welcome factor, the other side, the manifoldness of the members, must be reckoned with, and the right of representation must not be denied it on assumed but unstatable grounds. Otherwise, we have only said, -- and it is possible that we will have to be content with that -- that it is so because there are reasons for its being so.
There is, consequently, the temptation to use this second form of statement. The ideas which are conceived in one act of consciousness are, it is true, all bound together, but not in the same way. The strength of the union is, rather, a decreasing function of the time or of the number of intervening members. It is therefore smaller in proportion as the interval which separates the individual members is greater. Let a, b, c, d be a series which has been presented in a single conscious act, then the connection of a with b is stronger than that of a with the later c; and the latter again is stronger than that with d. If a is in any way reproduced, it brings with it b and c and d, but b, which is bound to it more closely, must arise more easily and quickly than c, which is closely bound to b, etc. The series must therefore reappear in consciousness in its original form although all the members of it are connected with each other.
Such a view as this has been logically worked out by Herbart. He sees the basis of the connection of immediately successive ideas not directly in the unity of the conscious act, but in something similar: opposed ideas which are forced together in a unitary mind can be connected only by partial mutual inhibition followed by fusion of what remains. Yet this, for our purpose, is not essential. He proceeds as follows:
"Let a series, a, b, c, d . . . be given in perception, then a, from the very first moment of the perception and during its continuance, is subjected to inhibition by other ideas present in consciousness. While a, already partially withdrawn from full consciousness, is more and more inhibited, b comes up. The latter, at first uninhibited, fuses with the retiring a. c follows and, itself uninhibited, is united with the fast dimming b and the still more obscured a. In a similar fashion d follows and unites itself in varying degrees with a, b, and c. Thus there originates for each of these ideas a law according to which, after the whole series has been forced out of consciousness for some tune, in its own way on its renewed appearance each idea struggles to call up every other idea of the same series. Suppose that a arises first, it is more closely connected with b, less with c, still less with d, etc. But, taken in the reverse order b, c, and d, all in an uninhibited condition, are fused with what remains of a. Consequently a seeks to bring them completely back to the form of an uninhibited idea; but its effect is quickest and strongest upon b, slower on c and still slower on d, etc. (whereby closer inspection shows that b sinks again while c is still rising, and that in the same way c sinks while d rises, etc.). In short, the series runs off as it was originally given. If we suppose, on the contrary, that c was the one initially reproduced, then its effect on d and the succeeding members is similar to that revealed by a -- i.e., the series c, d, . . . runs off gradually in conformity with its order. b and a, however, experience an altogether different influence. With their separate conscious residues, the uninhibited c had fused; its effect upon a and b was therefore without loss of power and without delay, but this effect was limited to bringing back the conscious residues of a and b bound up with it, only a part of b and a still smaller part of a being recalled to consciousness. This, then, is what happens if the process of recall begins anywhere at the middle of a known series. That which preceded the point of recall rises at once in graded degrees of clearness. That which followed, on the contrary, runs off in the order of the original series. The series, however, never runs backwards, an anagram is never formed out of a well understood word without voluntary effort."[1]
According to this conception, therefore, the associative threads, which hold together a remembered series, are spun not merely between each member and its immediate successor, but beyond intervening members to every member which stands to it in any close temporal relation. The strength of the threads varies with the distance of the members, but even the weaker of them must be considered as relatively of considerable significance.
The acceptance or rejection of this conception is clearly of great importance for our view of the inner connection of mental events, of the richness and complexity of their groupings and organisation. But it is clearly quite idle to contend about the matter if observation is limited to conscious mental life, to the registration of that which whirls around by chance on the surface of the sea of life.
For, according to the hypothesis, the threads which connect one member to its immediate successor although not the only one spun, are, however, stronger than the others. Consequently, they are, in general, as far as appearances in consciousness are concerned, the important ones, and so the only ones to be observed.
On the other hand, the methods which lie at the basis of the researches already described permit the discovery of connections of even less strength. This is done by artificially strengthening these connections until they reach a definite and uniform level of reproducibility. I have, therefore, carried on according to this method a rather large number of researches to test experimentally in the field of the syllable-series the question at issue, and to trace an eventual dependence of the strength of the association upon the sequence of the members of the series appearing in succession in consciousness.
Section 36. Methods of Investigation of Actual Behavior
Researches were again carried out with six series of 16 syllables each. For greater clearness the series are designated with Roman numbers and the separate syllables with Arabic. A syllable group of the following form constituted, then, each time the material for research:
I(1) I(2) I(3) . . . . . . . . . . . . . . . . . . . I(15) I(16)
II(1) II(2) II(3) . . . . . . . . . . . . . . . . . II(15) II(16)
.
.
.
VI(1) . . . . . . . . . . . . . . . . . . . . . . . . VI(15) VI(16)
If I learn such a group, each series by itself, so that it can be repeated without error, and 24 hours later repeat it in the same sequence and to the same point of mastery, then the latter repetition is possible in about two thirds of the time necessary for the first.[2] The resulting saving in work of one third clearly measures the strength of the association formed during the first learning between one member and its immediate successor.
Let us suppose now that the series are not repeated in precisely the same order in which they were learned. The syllables learned in the order I(1) I(2) I(3) . . . I(15) I(16) may for example be repeated in the order I(1) I(3) 1(5) . . . I(15) I(2) I(4) I(6) . . . I(16), and the remaining series with a similar transformation. There will first be, accordingly, a set composed of all the syllables originally in the odd places and then a set of those originally in the even places, the second set immediately following the first. The new 16-syllable series, thus resulting, is then learned by heart. What will happen? Every member of the transformed series was, in the original series, separated from its present immediate neighbor by an intervening member with the exception of the middle term where there is a break. If these intervening members are actual obstructions to the associative connection, then the transformed series are as good as entirely unknown. In spite of the former learning of the series in the original sequence, no saving in work should be expected in the repetition of the transformed series. If on the other hand in the first learning threads of association are spun not merely from each member to its immediate successor but also over intervening members to more distant syllables, there would exist, already formed, certain predispositions for the new series. The syllables now in succession have already been bound together secretly with threads of a certain strength. In the learning of such a series it will be revealed that noticeably less work is required than for the learning of an altogether new series. The work, however, will be greater than in relearning a given series in unchanged order. In this case, again, the saving in work will constitute a measure of the strength of the associations existing between two members separated by a third. If from the original arrangement of the syllables new series are formed by the omission of 2, 3, or more intervening members, analogous considerations result. The derived series will either be learned without any noticeable saving of work, or a certain saving of work will result, and this will be proportionally less as the number of intervening terms increases.
On the basis of these considerations I undertook the following experiment. I constructed six series of 16 syllables each with the latter arranged by chance. Out of each group a new one was then constructed also composed of six series of 16 syllables each. These new groups were so formed that their adjacent syllables had been separated in the original series by either 1, or 2, or 3, or 7 intervening syllables.
If the separate syllables are designated by the positions which they held in the original arrangement, the following scheme results:
I(1) I(2) I(3) . . . . . . . . . . . . . . . . . . . . . . . . I(15) I(16)
II(1) II(2) II(3) . . . . . . . . . . . . . . . . . . . . . . II(15) II(16)
.
.
.
VI(1) VI(2) VI(3) . . . . . . . . . . . . . . . . . . . . VI(15) VI(16)
By using the same scheme the derived groups appear as follows:
By Skipping 1 Syllable
I(1) I(3) I(5) . . . . . . . I(15) I(2) I(4) I(6) . . . . . . . I(16)
II(1) II(3) II(5) . . . . . II(15) II(2) II(4) II(6) . . . . . II(16)
.
.
.
VI(1) VI(3) . . . . . . . VI(15) VI(2) VI(4) . . . . . . . VI(16)
By Skipping 2 Syllables
I(1) I(4) I(7) I(10) I(13) I(16) I(2) I(5) I(8) I(11) I(14) I(3) I(6) I(9) I(12) I(15)
II(1) II(4) I(7) . . . . . . . .II(16) II(2) II(5) . . . . . . II(14) II(3) II(6) . . . . . . .II(15)
.
.
.
VI(1) VI(4) . . . . . . . . . VI(16) VI(2) VI(5) . . . . . VI(14) VI(3) VI(6) . . . . . VI(15)
By skipping 3 syllables
I(1) I(5) I(9) I(13) I(2) I(6) I(10) I(14) I(3) I(7) I(11) I(15) I(4) I(8) I(12) I(16)
II(1) II(5) . . . . . . II(2) II(6) . . . . . . . II(3) II(7) . . . . . . . . II(4) II(8). . . . .II(16)
.
.
.
VI(1) VI(5) . . . . . VI(2) VII(6) . . . . . . VI(3) VI(7) . . . . . . . VI(4) II(8). . . . VI(16)
By Skipping 7 Syllables
I(1) I(9) II(1) II(9) III(1) III(9) IV(1) IV(9) V(1) V(9) VI(1) VI(9) I(2) I(10) II(2) II(10)
III(2) III(10) IV(2) IV(10) V(2) V(10) VI(2) VI(10) I(3) I(11) II(3) II(11)III(3) III(11) IV(3) IV(11)
.
.
.
V(7) V(15) I(8) I(16) II(8) II(16) III(8) III(16) IV(8) IV(16) V(8) V(16) VI(8) VI(16)
As a glance at this scheme will show, not all the neighboring syllables of the derived series were originally separated by the number of syllables designated. In some places in order to again obtain series of 16 syllables1 greater jumps were made; but in no case was the interval less. Such places are, for example, in the series in which two syllables are skipped, the transitions from I(16) to I(2) and from I(14) to I(3). In the series in which 7 intermediates were jumped, there are seven places where there was no previous connection between successive syllables since the syllables in question came from different series and the different series, as has been often mentioned, were learned independently. The following is given in illustration: I(9) II(1), II(9) III(1), etc. The number of these breaks varies with the different kinds of derivation, but in each case is the same as the number of skipped syllables. On account of this difference, the derived series suffer from an inequality inherent in the nature of the experiment.
In the course of the experiment the skipping of more than 7 syllables was shown to be desirable, but I refrained from carrying that out. The investigations with the six 16-syllable series were carried quite far; and if series had been constructed using greater intervals, the breaks above mentioned would have had too much dominance. The derived series then contained ever fewer syllable-sequences for which an association was possible on the basis of the learning of the original arrangement; they were ever thus more incomparable.
The investigations were carried on as follows: -- Each time the six series were learned in the original order and then 24 hours later in the derived and the times required were compared. On account of the limitation of the series to those described above the results are, under certain circumstances, open to a serious objection. Let it be supposed that the result is that the derived series are actually learned with a certain saving of time, then this saving is not necessarily due to the supposed cause, an association between syllables not immediately adjacent. The argument might, rather, run as follows. The syllables which are first learned in one order and after 24 hours in another are in both cases the same syllables. By means of the first learning they are impressed not merely in their definite order but also purely as individual syllables; with repetition they become to some extent familiar, at least more familiar than other syllables, which had not been learned just before. Moreover the new series have in part the same initial and final members as the old. Therefore, if they are learned in somewhat less time than the first series required, it is not to be wondered at. The basis of this does not necessarily lie in the artificial and systematic change of the arrangement, but it possibly rests merely on the identity of the syllables. If these were repeated on the second day in a new arrangement made entirely by chance they would probably show equally a saving in work.
In consideration of this objection and for the control of the remaining results I have introduced a further, the fifth, kind of derived series. The initial and final syllables of the original series were left in their places. The remaining 84 syllables, intermediates, were shaken up together and then, after chance drawing, were employed in the construction of new series between the original initial and final series. As a result of the learning of the original and derived series there must in this can also be revealed how much of the saving in work is to be ascribed merely to the identity of the syllable masses and to the identity of the initial and final members of the separate series.
Section 37. Results. Associations of Indirect Sequence
For each group of original and derived series 11 double tests were instituted, 55 therefore in all. These were distributed irregularly over about 9 months. The results were as follows:

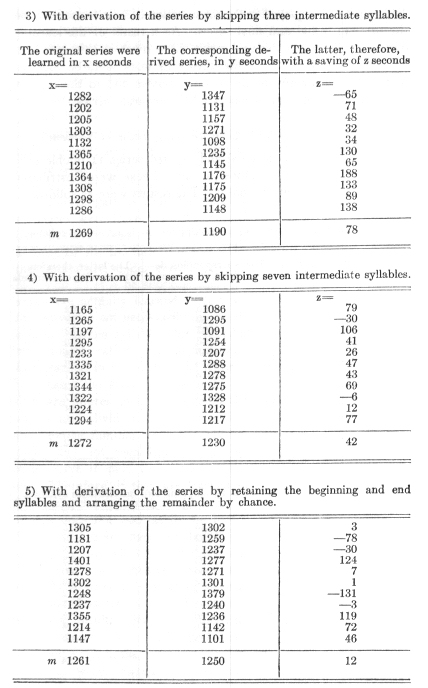
To summarize the results: The new series- formed by skipping 1, 2, 3 and 7 intermediate members were learned with an average saving of 152, 94, 78 and 42 seconds. In the case of the construction of a new series through a mere permutation of the syllables, there was an average saving of 12 seconds.
In order to determine the significance of these figures, it is necessary to compare them with the saving in work in my case in the relearning of an unchanged series after 24 hours. This amounted to about one third of the time necessary for the first learning in the case of 16-syllable series, therefore about 420 seconds.
This number measures the strength of the connection existing between each member and its immediate sequent, therefore the maximal effect of association under the conditions established. If this is taken as unity, then the strength of the connection of each member with the second following is a generous third and with the third following is a scant fourth.
The nature of the results obtained confirm -- for myself and the cases investigated -- the second conception given above and explained by means of a quotation from Herbart. With repetition of the syllable series not only are the individual terms associated with their immediate sequents but connections are also established between each term and several of those which follow it beyond intervening members. To state it briefly, there seems to be an association not merely in direct but also in indirect succession. The strength of these connections decreases with the number of the intervening numbers; with a small number it was, as will be admitted, of surprising and unanticipated magnitude.
No evidence has been secured, however, establishing the facilitation of the process of relearning a series by means of the identity of the syllables and the identity of the initial and final terms.
Section 38 Experiments with Exclusion of Knowledge
I have hitherto not stated the probable errors of the results, in order to discuss their reliability more fully at this time.
When I started upon the experiment I had no decided opinion in favor of the final results. I did not find facilitation of the learning of the derived series essentially more plausible than the opposite. As the numbers more and more bespoke the existence of such facilitation, it dawned upon me that this was the correct and natural thing. After what has been said above (p. 27ff [middle of chapter III]) one might think that in the case of the remaining experiments, this idea has possibly favored a more attentive and therefore quicker learning of the derived series, and so has, at least, decidedly strengthened the resulting saving in work, even if it has not caused it altogether.
For the three largest of the numbers found, -- consequently, for the facilitation of the work which took place in the case of the omission of 1, 2, and 3 intervening syllables -- this objection is of slight significance. For these are proportionately so large that it would be attributing too much to an involuntary heightening of a state of attention, voluntarily concentrated without this to the utmost, if an actual influence is ascribed to it here. Moreover, the gradation of the numbers, decisively issuing as they do from the distribution of the individual values and running parallel with the number of skipped intermediate terms, is inconceivable on any such hypothesis as this. For the supposed greater concentration of the attention could clearly work only in general. How could it possibly bring about so regular a gradation of numbers in the case of tests which were separated from each other by weeks and months?
The objection presented above could render doubtful only the fourth result, the proportionally slight saving in the learning of series formed from other series by skipping seven intermediate terms.
Clearly in this case the exact determination of the difference is of especial interest because of the significant size of the interval over which an association took place.
In the case of the present investigations there exists the possibility of so arranging them that knowledge concerning the outcome of the gradually accumulating results is excluded and so that consequently the disturbing influence of secret views and desires disappears. I have accordingly instituted a further group of 30 double tests in the following way as a control of the above results, and especially of the least certain of them.
On the front side of a page were written six syllable series selected by chance and on the reverse side of the same sheet six series formed from them by one of the methods of derivation described above (p.97 [Section 36]). For each of the five transformations 6 sheets were prepared. The fronts and backs of these could be easily distinguished but not the sheets themselves. The thirty sheets were shuffled together and then laid aside until any memory as to the occurrence of the separate syllables in definite transformations could be considered as effaced. Then the front side, and 24 hours later, the reverse side of a given sheet were learned by heart. The times necessary for learning the separate series were noted, but they were not assembled and further elaborated until all 30 sheets had been completed. Following are the numbers.

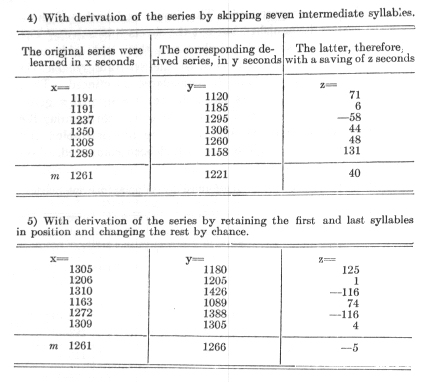
By derivation of the transformed series by skipping 1, 2,3, 7 intermediate syllables, the derived series were therefore learned with an average saving of 110, 79, 64 40 seconds. On the contrary with derivation of the series by permutation of the syllables the learning required an average increase in expenditure of 5 seconds.
Taken as a whole, these last results exactly confirm, as can be seen, the result that was obtained at the beginning. The number of these experiments was proportionally small and, during the course of each experiment, there was complete exclusion of knowledge as to results. In spite of these facts and although the numbers, considered individually, seem to be distributed without regard to law, their grouping, when taken as a whole, is seen to be in conformity to a simple law. The fewer are the intervening members which separate two syllables of a series which has been learned by heart, the less is the resistance offered by these separated syllables to their being learned in a new order. And, in the same way, the fewer are these intervening terms, the stronger are the bonds which, as a result of the learning of the original series, connect the two syllables across the intervening members.
In addition to agreeing in their general course, the numbers for both groups of experiments also agree in the following respect. The difference between the first and second numbers has the greatest value, and that between the second and third has the least value. On the other hand, it is surprising that, with respect to their absolute size, the numbers of the second group are throughout smaller than those of the first. Two causes may be brought forward in explanation of this behavior, which, considering the conformity of the numbers, can scarcely be accidental. It may be that here is actually revealed that influence of expectation which has already been mentioned. On the basis of this hypothesis, the explanation of the fact that the numbers of the first group come out somewhat too large is that, in the course of the experiment, the existence of a saving in work in the case of the derived series was anticipated, and for this reason the learning of the series took place involuntarily with a somewhat greater concentration of attention. On the other hand, it may be that, in consequence of the excluded knowledge, there has been at work in the case of the numbers of the second group a disturbing element which has made them smaller. Here, to be sure, during the learning of the derived series a very lively curiosity developed concerning the category of transformation to which the series which had just been learned belonged. That this must have had a distracting, and therefore retarding, influence is probable not only in itself but also through the result obtained from the series derived by permutation of syllables. It was to be expected that the identity of the syllables, as well as of the initial and end terms, would make itself felt in this case by a saving of work, however small that saving might be. The latter effect appears, it is true, in the experiments of the first group. With those of the second group, however, there is noticeable, instead of this saving of work, a slight additional expenditure of time. This, if it is not merely accidental, can scarcely be explained otherwise than through the distracting curiosity mentioned.
It is possible that both influences were at work simultaneously so that the first experiments gave results which were somewhat too high; and the second, results that were somewhat too low. It is allowable, under this hypothesis, to put the two sets of figures together so that the contrasting errors may compensate each other. In this way there was finally obtained out of the 85 double tests the following table.
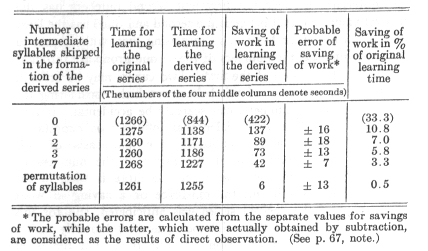
Section 39. Discussion of Results
In the foregoing table an especial interest, it seems to me, is connected with the last, and also with the next to the last, row of numbers. When there was complete identity of all the syllables and the initial and end terms were left in their places, the average saving of time for 17 tests dealing with the learning of the derived series was so slight that it was hardly to be determined. It fell within half of its probable error. The syllables were, therefore, in themselves, outside of their connection, so familiar to me that they did not become noticeably more familiar after being repeated 32 times. On the contrary when a related series was repeated the same number of times, each syllable became so firmly bound to the syllable which followed 8 places beyond that 24 hours later the influence of this connection could be determined in no doubtful fashion. It attains a value 6 times the probable error. Its existence, therefore, must be considered to be fully proved although naturally we cannot be so sure that its size is exactly what it was found to be in the experiments. Although its absolute value is small, yet its influence amounts to one tenth of that of the connection which binds every member to its immediate successor. It is so significant, and at the same time the decrease in the after-effect of connections which were formed over 2, 3, 7 intervening members is so gradual a one, that the assertion can be made, am these grounds alone, that even the terms which stand still further from one another may have been bound to each other subconsciously by threads of noticeable strength at the time of the learning of the series.
I will summarise the results so far given in a theoretical generalisation. As a result of the repetition of the syllable-series certain connections are established between each member and all those that follow it. These connections are revealed by the fact that the syllable-pairs so bound together are recalled to mind more easily and with the overcoming of less friction than similar pairs which have not been previously united. The strength of the connection, and therefore the amount of work which is eventually saved, is a decreasing function of the time or of the number of the intervening members which separated the syllables in question from one another in the original series. It is a maximum for immediately successive members. The precise character of the function is unknown except that it decreases at first quickly and then gradually very slowly with the increasing distance of the terms.
If the abstract but familiar conceptions of 'power,' 'disposition,' be substituted for the concrete ideas of saving in work and easier reproduction, the matter can be stated as follows. As a result of the learning of a series each member lass a tendency, a latent disposition, to draw after itself, at its own return to consciousness, all the members of the series which followed it. These tendencies are of varying strength. They are the strongest for the members which immediately follow. These tendencies are accordingly in general most easily demonstrable in consciousness. The series will return in its original form without the intervention of other influences while the forces directed to the resuscitation of the remaining members can be explicitly demonstrated only by the introduction of other conditions.
It is naturally not conceivable that by a mere caprice of nature the validity of the principles discovered should be limited exclusively to the character of the material in which they were obtained -- i.e., to series of nonsense syllables. They may be assumed to hold in an analogous way for every kind of idea-series and for the parts of any such series. It goes without saying, wherever relations exist between the separate ideas, other than those of temporal sequence and separation by intermediate members, these forces will control the associative flow, not exclusively, but with reference to all the modifications and complications introduced by relations of various affinities, connection, meaning, and the like.
At any rate, it will not be denied that the doctrine of Association would gain through a general validity of these results a genuine rounding out and, so to say, a greater reasonableness. The customary formulation, "ideas become associated if they are experienced simultaneously or in immediate succession," has something irrational about it. If the immediacy of succession is taken precisely, the principle contradicts the most common experiences. If it is not taken exactly, then it is hard to state what kind of sequence is properly meant At the same time it is not clear why a sequence not quite direct should have an advantage which suddenly disappears in the case of a sequence still more indirect. As we now know, the directness or indirect-ness of the sequence is without effect upon the general nature of what happens between ideas which succeed each other. In both cases connections are formed which on account of their complete similarity can be designated only by the common term, Association. But these are of different strength. As the succession of united ideas approaches ideal immediacy the connecting threads grow stronger, and in proportion as it departs from this ideal, these threads grow weaker. The associations between more distant terms, although actually present and demonstrable under proper conditions have, nevertheless, on account of their slight strength, practically no significance. The associations between adjacent terms are, on the contrary, of relatively great importance, and will make their influence abundantly felt. Of course, if the series were left entirely to themselves and if they were always produced in precisely the same order, for each term there would appear only one association, the relatively strongest -- namely, that with the immediately succeeding term. But series of ideas are never left to themselves. The rich and quickly changing order of events brings them into the most manifold relations. They return with their members in the most varied combinations. And then, under certain circumstances, the stronger of these less strong associations between more distant terms must find opportunity to authenticate their existence and to enter into the inner course of events in an effective way. It is easy to see how they must favor a more rapid growth, a richer differentiation, and a many-sided ramification of the ideas which characterise the controlled mental life. Of course they also favor a greater manifoldness, and so apparently a greater arbitrariness and irregularity, in mental events.
Before I proceed further, I wish to add a few words concerning the above mentioned (p.91 [Section 35]) derivation of the association of successive ideas from the unitary consciousness of a unitary soul. There is a certain danger in bringing together a present result with one found previously. I mentioned above (p.47 [beginning of Chapter V]) that the number of syllables which I can repeat without error after a single reading is about seven. One can, with a certain justification, look upon this number as a measure of the ideas of this sort which I can grasp in a single unitary conscious act. As we just now saw, associations are formed of noticeable strength over more than seven intervening members, therefore between the beginning and end of a nine-syllable series. And on account of the size of the numbers obtained and the nature of their gradation, it seems probable that, even with a larger number of syllables, connections would be formed between their extremes. If, however, associations are built between members too far separated to be held together in a single conscious act, it is no longer possible to explain the presence of those associations on the basis of the simultaneous presence of the united ideas in consciousness.
However, I recognise that those for whom such a derivation is a cherished matter are not necessarily forced by the above discussion to abandon their conception. Such are those who consider the unitary acts of a unitary soul as something more original, intelligible, transparent or better worthy of belief than the simple facts of association described above, so that the reduction of the latter to the former would be a noteworthy achievement. One needs but to say that, in the case of an unfamiliar sequence of syllables, only about seven can be grasped in one act, but that with frequent repetition and gradually increasing familiarity with the series this capacity of consciousness may be increased. So, for example, a series of 16 syllables, which have been thoroughly memorised, may be present in a single conscious act. Accordingly this "explanation" is freely available. Those for whom it was of value in the case of association by simultaneity or immediate succession can employ it fully as well for our case of indirect sequence. And because of the modest requirements which in psychology are so often imposed upon explanations, this view will doubtless for a long time serve to make dim the vision and so prevent the frank recognition of this as one of the most wonderful of all riddles, and it will also act as a hindrance in the search for its true understanding.
Section 40. Reverse Associations
Of the many problems which spring out of the results presented I have been able for the time being to investigate only a few and these by means of only a small number of experiments.
As a result of the frequent repetition of a series -- a, b, c, d . . . -- certain connections -- ab, ac, ad, bd, etc. -- are formed. The idea a, whenever and however it returns to consciousness, has certain tendencies of different strength to bring also with it to consciousness the ideas b, c, d. Are now these connections and tendencies reciprocal? That is, if at any time c and not a is the idea by some chance revived, does this have, in addition to the tendency to bring d and e back with it, a similar tendency in the reverse direction towards b and a? In other words: -- As a result of the previous learning of a, b, c.[sic] d, the sequences a, b, c, a, c, e, are more easily learned than any grouping of equal length of syllables previously unknown such as p, q, r. . . . Is the same thing true of the sequences c b a, and e c a? As a result of manifold repetition of a series are associations also formed in the reverse order?
The views of the psychologists seem to be divergent upon this point. One side call attention to the undoubted fact that in spite of complete mastery of, say, the Greek alphabet a person is not at all in a position to repeat it readily backwards if he has not specially studied and practiced it in this form.
The other side make extensive use of reverse associations, as of something quite intelligible, in their explanation of the origin of voluntary and purposive movements. According to them the movements of the child are at first involuntary and accidental. With certain combinations of these, intensely pleasurable feelings result. In the case of movements as of feelings, memory traces remain which, by repetition of the occurrences, are always more closely associated with each other. If this connection has attained a certain strength, the mere idea of the agreeable feeling leads backwards to the idea of the movement which aroused it; then comes the actual movement and with it also the actual sensed feeling.
The conception of Herbart, which we learned to know above (p. 94 [Section 35]), holds the middle course between these two views. The idea c, which appears in the course of a series, fuses with the ideas b and a, which have preceded it and which are yet present although becoming dim. If c is later on reproduced, it brings b and a with it but dimmed, not fully uninhibited or clearly conscious. With the sudden arousal of a member out of the midst of a series we survey that which preceded "at once in graded clearness"; but never does it happen that the series runs off in reverse order. To the member which springs up in consciousness there succeed in due order and in complete consciousness those terms which followed it in the original series.
For the purpose of testing the actual relations I carried out an experiment entirely similar to the previously described investigations. Out of groups each composed of six 16-syllable series arranged by chance new groups were derived either through mere reversal of the sequence or by that plus the skipping of an intermediate syllable. Then the two sets of groups were learned by heart, the derived form 24 hours later than the original.
If the scheme for the original form is written as follows:
I(1) I(2) 1(3) . . . . . . . I(15) I(16), then the corresponding derived series is thus designated:
In the case of mere reversal of the syllable sequence;
I(16) I(15) I(14) . . . . . . . . I(2) I(1),[sic]
In the case of reversal plus skipping of an intermediate syllable,
I(16) I(14) I(12). . . . . . . I(4) I(2) I(15) I1(13). . . . . . . I(3)I(1).
For the first kind of derivation I have carried out ten experiments; for the second, only four.
The results are as follows:

In relation to the time of learning the original series the saving amounts to 124 per cent.

In relation to the time of learning the original series the saving amounted to ~ per cent.
As a result of the learning of a series certain connections of the members are therefore actually formed in a reverse as well as in a forward direction. These connections are revealed in this way, that series which are formed out of members thus connected are more easily learned than similar series, whose individual members are just as familiar but which have not been previously connected. The strength of the predispositions thus created was again a decreasing function of the distance of the members from each other in the original series. It was, however, considerably less for the reverse connections than for the forward ones, the distances being equal. With an approximately equal number of repetitions of the series the member immediately preceding a given member was not much more closely associated with it than the second one following it; the second preceding -- so far as may be determined on the basis of these few researches -- scarcely as firmly as the third following.
If one could assume a more general validity for this relation found here first in connection with syllable series, the mutually opposed experiences just mentioned would, I believe, become thoroughly intelligible. Where a series consists of only two members -- as in the case of the connection between a simple idea of movement and that of an agreeable feeling -- then, by means of frequent repetition the end term will acquire so strong a tendency to call up after itself the initial term that the latter will actually appear. For the bringing up of the term first preceding it is the only thing for which, as a result of the many repetitions, the second term has acquired a predisposition. But, no matter how many repetitions there may be in the case of a long series, it will never happen on the arousal of a middle term that the series will reappear in a reverse order. For, however easily the immediately preceding term may connect itself with the one for the moment aroused, the immediately succeeding term will appear more easily by far, and so will win the victory, provided other influences do not intervene.
No matter how thoroughly a person may have learned the Greek alphabet, he will never be in a condition to repeat it backwards without further training. But if he chances to set out purposely to learn it backwards, he will probably accomplish this in noticeably shorter time than was the case in the previous learning in the customary order. The objection is not in point that a poem or speech which has been committed to heart is not necessarily learned more quickly backwards than it was originally forwards. For with the learning in reverse direction the numerous threads of inner connection on which rapid learning of meaningful material in general depends will be brought to nothing.
Section 41. The Dependence of Associations of Indirect Sequence upon the Number of Repetitions
The connection set up as a result of many repetitions between the immediately succeeding members of an idea- or syllable-series is a function of the number of repetitions. As a result of the investigations of Chapter VI, which were purposely directed to the discovery of this relation, an approximate proportionality, within tolerably wide limits, has been made out between the number of repetitions and the strength of the connections established by them. The latter was measured, precisely as in the investigations of the present chapter, by the amount of work saved in relearning the connected series after 24 hours.
If now, as a result of repetitions, connections are also set up between members of a series which are not immediately successive, the strength of the latter is naturally also in some way dependent upon the number of repetitions. The question arises in what form the different dependence occurs in this case. Does a proportionality exist here also? If the number of repetitions is made greater, will the threads of separate strength, which bind together all the members of a series learned by heart, increase in strength in the same proportion? Or is the nature and rate of their increase in strength a different one as is the case with the strength of the threads themselves? On the basis of our present knowledge neither the one nor the other of these possibilities can be declared self-evident
To facilitate an insight into the actual conditions I have instituted a few preliminary experiments in the following way. Six aeries of 16 syllables each were impressed upon the memory by a 16- or 64-fold attentive repetition. After 24 hours an equal number of derived series of the same length, which had been obtained from those already learned by skipping one intermediate syllable, were learned by heart to the first repetition. In order to make the investigations useful in other ways, the series were derived in this case by a method somewhat different from that described above (p. 97 [Section 36]). The latter method differs from the former in that here the odd-numbered syllables of the original series were not followed by the even-numbered syllables of the same series. But all the odd-numbered syllables of two original series were united to form a new 16-syllable series. Then the even-numbered syllables of the same original series were united to form a second new series. The scheme of the derived series was therefore not, as above,
I(1) I(3) I(5) . . . . . . . . . . I(15) I(2) I(4) . . . . . I(16)
II(1) II(3) II(5) . . . . . . . . II(15) II(2) II(4) .. . . . II(16)
but rather
I(1) I(3) I(5) . . . . . . . . . . I(15) II(1) I(3) . . . . . I(15)
I(2) I(4) I(6) . . . . . . . . . I(16) II(2) II(4) . . . . . II(16)
The effect of the derivation upon the learning of the derived series, cannot, as it seems, be essentially affected through this slight change. Here, as in the above described method of derivation, the syllables which during the first learning had been separated from each other by an intervening syllable were learned 24 hours later in immediate succession.
For each number of repetitions used in learning I made 8 double tests, which gave the following results:
Number of repetitions employed for the impression of each of the original series:
|
16 |
64 |
Number of seconds required for learning the six derived series after 24 hours (including the recital):
|
1178 |
1157 |
|||
|
1216 |
982 |
|||
|
1216 |
1198 |
|||
|
950 |
1148 |
|||
|
1358 |
995 |
|||
|
1019 |
1017 |
|||
|
1191 |
1183 |
|||
|
1230 |
1198 |
|||
|
--------------- |
||||
|
Average |
1170 |
1109 |
||
|
Probable error |
30 |
22 |
||
On account of the small number of experiments the resulting averages are, unfortunately, not very exact; but the general character of the results would remain the same even if we considered the value false within the whole range of the probable error. This character becomes apparent upon comparison with the values given above (p.56 [middle of Chapter 6]) for learning by heart six 16-syllable series which had not previously been learned. This took place in 1,270 seconds. After the original series had been repeated 16 times, the derived series was learned with a saving of about 100 seconds; after repetition 64 times, with a like saving of 161 seconds. Quadrupling the repetitions resulted in increasing the saving only a little more than half as much again. The increase in strength of the associations reaching over an intermediate member was in nowise proportional to the number of repetitions, for the cases studied, not even within the limits for which this was noticeably the case for associations from one member to its immediate successor. On the contrary the effect of the repetitions in the case of associations of indirect sequence decreased considerably sooner and more quickly than in the case of those of direct sequence.
There is very close agreement between the pair of values just found and the number given above (p.99, I [Section 37]) -- the procedure being, as here, without the exclusion of knowledge -- for the learning of derived series which the day before had been learned in their original form to the point of first possible reproduction. This number, it is true, was obtained under somewhat different conditions. In the first place, not always were the same number of repetitions employed for learning, but each time as many as were required for the first possible reproduction -- i.e., not exactly, but on the average, 32. Moreover, the nature of the derivation of the senses was somewhat different, as was stated above. But these differences have little weight in the case of numbers which otherwise could have little claim to exactness. I adduce therefore this value for comparison, and in addition the numbers give in Chapter VI for the influence of repetitions on the relearning of the same untransformed series. Here then is the table.

I call attention again to the fact that the numbers given above are in part rather inexact and that they were gained under very limited conditions. However, it is allowable to sketch summarily and with hypothetical elaboration the view which these results make appear to be the most probable explanation of an important group of inner processes and which fills pleasingly and completely a hitherto empty place in our knowledge.
With the imprinting and internal fixation of an idea-series through its manifold repetition, inner connections, associations, are woven between all the separate members of the series. The nature of these is such that series made out of members thus associated are picked up and reproduced more easily, with less resistance to be overcome, than similar series made up of members not previously associated. Their nature can also be stated in this way, that each member of the series has the definite tendency on its own return to consciousness to bring back others with it. These connections, or tendencies, are of different strength from several different points of view. For the more distant members of the original series they are weaker than for the nearer; for specific distances backwards they are weaker than for the same distances forward. The strength of all the connections increases as the number of repetitions increases. But the originally stronger threads between the nearer members are strengthened considerably more quickly than the weaker ones which connect the more distant terms. The more, therefore, the number of repetitions increases, the stronger, both absolutely and relatively, become the connections between immediately successive terms. To the same degree the more exclusive and dominant becomes the tendency of each term at its own return into consciousness to draw after itself that term which had always immediately followed it during the repetitions.
Section 42. Indirect Strengthening of Associations
I conclude with the mention of a noteworthy fact which appeared incidentally in connection with the investigations mentioned in the preceding paragraphs. On account of the uncertainty of the numerical results which come into consideration, I can call attention to it only with great reserve. I cannot, how-ever, pass it by altogether because it is probable in itself, and because, with further confirmation, it will throw a characteristic light on inner processes which are actually present but which remain unconscious. It will also reveal the relative independence of these processes from conscious accompaniments, as I have shown above (§ 24).
The derivation of the transformed series in the case of the last mentioned investigations was accomplished, as has been stated, in the following way. Out of two 16-syllable series selected by chance, first all the odd-numbered syllables were combined to form a new series and then all the even-numbered to form a second series which followed in immediate succession. In the case of a group consisting of six series of this sort, therefore, the derived series II contained nothing but syllables which in the first process of memorising had followed immediately upon the corresponding members of series I. The derived series IV bore a similar relation to series III, and series VI to series V. The following phenomenon appeared, which is the peculiar relation to which I wish to call attention. Less time was required for learning by heart series II, IV, VI on the average than for series I, III, V, although in all the other groups of series, whether original or derived, the converse was the case.
I adduce some numerical data in evidence of this relation.
From all the experiments with six series of 16 syllables which were learned to the point of the first recital, ten immediately successive experiments are chosen by chance for two different time-periods. The times for committing to memory series I, III, V are combined in calculation, as are also those for series II, IV, VI.
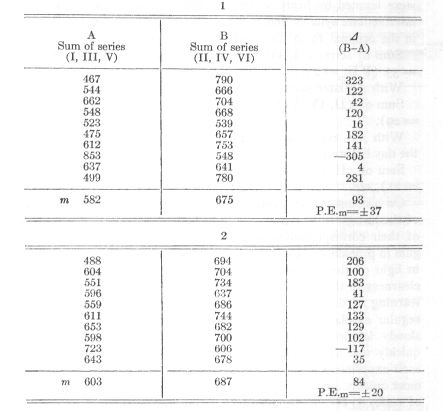
The sum of series II, IV and VI, found by averaging the ten experiments, is here in both cases, as can readily be seen, considerably greater than the sum of series I, III, V. The differences are, to be sure, of very different amounts for the separate experiments, and in one case they have a pronounced negative value; but these fluctuations are represented in the large probable error of the differences of the averages; and, in spite of the size of these errors, the positive character of the differences may be considered as fairly certain.
In all other investigated cases the following result appears: there are large fluctuations of the differences in the individual experiments, but a combination of the several experiments shows a decisive predominance for series II, IV, VI although the surplus is smaller than in the case of the two experiments in question. Thus in the case of it earlier tests in which series were learned by heart which had been derived by skipping one intermediate syllable and which had been learned the day before in the original form the results were (p.99, I [Section 37]):
Sum of series (II, IV, VI) minus Sum of series (I, III, V) = 33 (P.E.m = 23)~
With six later tests of the same sort (p.103, I [Section 37]):
Sum of (II, IV, VI) minus Sum of (I,III, V) = 42 (P.E.m = 29).
With ten experiments with series which had been repeated the day before 16 times each (p. 55 [beginning of Chapter 6]):
Sum of (II, IV, VI) minus Sum of (I, III, V) = 17 (P.E.m = 21), etc.
On account of the largeness of the probable error a single one of the last given figures would have little significance. By means of their correspondence as to the nature of the difference they gain in probability, and the phenomenon becomes quite intelligible in light of the results of Section 18. There, and with especial dearness in the case of 16-syllable series, it was shown that the learning of the individual series occurred in the form of fairly regular oscillations. These were of such a sort that a relatively slowly learned series followed one learned relatively more quickly and vice versa (p.43 [end of Chapter 4], Fig. 3). Since in the case of each experiment the first series was learned on the average the most quickly and the second the most slowly, by the combination of series I,III, V the average minima are united and of series II, IV, VI the average maxima. The difference, S (II, IV, VI) minus (I,III, V) is, therefore, in general positive.
Accordingly it must be surprising that in the case of both the groups of tests mentioned in the preceding paragraphs, this difference is on the contrary of a negative sign.

The fluctuations of the numbers for the separate experiments are also in this case very great. However, it is evident on the first glance and without further comparison that a strong displacement of the differences to the negative side has taken place. This fact is also expressed by the averages. In contrast with previous results, the series II, IV, VI were learned in somewhat shorter time than series I, III, V.
That this exception rests on mere chance is possible but not very probable. The probable errors, although large, are not large enough to indicate this.
I would sooner fear that it was a case of disturbance of the results through the oft-mentioned source of error, anticipation of the outcome (p.27 ff. [Chapter III] and p. 101[Section 37]). During the progress of the experiment I believed with increasing certainty that I could foresee the smaller expenditure of time for the learning of series II, IV, VI, and it was only because I thought something of this sort that I changed the method of derivation of the transformed series. I cannot, therefore, exclude the possibility that, merely on the basis of this hidden presupposition and in a manner altogether unrevealed to consciousness, a greater concentration of attention was present in learning series II, IV, VI than in learning series I, III, V. However, this assumption is not to be taken positively as the correct one. The assumption that the whole of the difference found is to be traced back to the influence of this source of error would involve the ascription of a pretty large function to an involuntary and completely unconscious accommodation of attention due to a secret expectation.
There remains, accordingly, a certain probability for the third possibility, namely, that the contrasting character of the average differences has in part at least an objective basis, that the more rapid learning of the derived series, II, IV, VI, was in part due to their manner of derivation.
The proper way in which to think of this causation would become dear only by the introduction of physiological conceptions which must first be constructed or at least remodelled. If use is made of the language of psychology, then, as in the case of all unconscious processes, expression can be only figurative and inexact.
As a result of the learning by heart of a series in the original form the separate syllables, we must say, retain fairly strong tendencies upon their own return to consciousness to bring after them the syllables which immediately succeeded them. If, therefore, the syllables 1, 3, 5, etc., return to consciousness, the syllables 2, 4, 6, etc., have a tendency also to appear. This tendency is not strong enough to bring about as a consciously perceivable event the actual appearance of 2, 4, 6. The latter are in evidence only in a certain inner condition of excitability; something takes place in them which would not have occurred if 1, 3, 5 had not been repeated. They behave like a forgotten name which one attempts to recollect. This is not consciously present; on the contrary, it is being sought. In a certain way, however, it is undeniably present. It is on the way to consciousness, as one might say. For if ideas of all sorts were called up which stood in connection with the earlier experienced name, a person could usually tell whether they agreed with the one now sought for but not yet found, or not. As a result of the frequent repetition of the syllables 1, 3, 5 previously connected with the syllables 2, 4, 6, the latter were placed in a similar slightly pronounced condition of excitation, lying between conscious appearance on the one side and simple non-appearance on the other. And this excitation has, as it now appears from our tests, a result altogether similar to that of actual return to consciousness. Inner connections are established between successively and internally aroused syllables just as between syllables successively raised to consciousness, except that the former are naturally of less strength. Secret threads are spun which bind together the series 2, 4, 6, not yet aroused to consciousness, and prepare the way for its conscious appearance. Such threads existed already in greater strength as a result of the learning of the original series; the present effect is that of strengthening somewhat connections already made. And that is nothing else than what was found above: if two syllable-combinations -- 1, 3, 5 . . . and 2, 4, 6 . . . -- are frequently associated in consciousness (the learning of the original series) then the subsequent learning of the second combination (derived series II, IV, VI) soon after the learning of the first (derived series I, III, V) has considerably less resistance to overcome than the latter. A certain strengthening of associations takes place, not only directly, through conscious repetition of the associated members, but also indirectly through the conscious repetition of other members with which the first had been frequently connected.
This way of viewing the matter is a consequence of the assumption (which became necessary above, p. 109 [Section 39]) of the formation of associative connections over more intervening members than could be comprehended in one clearly conscious act. These connections would be very fruitful in the explanation of many surprising phenomena of memory and recollection, but on account of the uncertainty of their experiential basis I refrain for the present from pursuing them further.
Footnotes