An internet resource developed by
(Return to index)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER VII
RETENTTON AND OBLIVISCENCE AS A FUNCTION OF THE TIME
Section 26. Exp1anations of Retention and Obliviscence
All sorts of ideas, if left to themselves, are gradually forgotten. This fact is generally known. Groups or series of ideas which at first we could easily recollect or which recurred frequently of their own accord and in lively colors, gradually return more rarely and in paler colors, and can be reproduced by voluntary effort only with difficulty and in part. After a longer period even this fails, except, to be sure, in rare instances. Names, faces, bits of knowledge and experience that had seemed lost for years suddenly appear before the mind, especially in dreams, with every detail present and in great vividness; and it is hard to see whence they came and how they managed to keep hidden so well in the meantime. Psychologists -- each in accordance with his general standpoint -- interpret these facts from different points of view, which do not exclude each other entirely but still do not quite harmonise. One set, it seems, lays most importance on the remarkable recurrence of vivid images even after long periods. They suppose that of the perceptions caused by external impressions there remain pale images, "traces," which, although in every respect weaker and more flighty than the original perceptions, continue to exist unchanged in the intensity possessed at present. These mental images can not compete with the much more intense and compact perceptions of real life; but where the latter are missing entirely or partly, the former domineer all the more unrestrainedly. It is also true that the earlier images are more and more overlaid, so to speak, and covered by the later ones. Therefore, in the case of the earlier images, the possibility of recurrence offers itself more rarely and with greater difficulty. But if, by an accidental and favorable grouping of circumstances, the accumulated layers are pushed to one side, then, of course, that which was hidden beneath must alppear, after whatever lapse of time, in its original and still existent vividness.[1]
For others[2] the ideas, the persisting images, suffer changes more and more affect their nature; the concept of obscuration comes in here. Older ideas are repressed and forced to sink down, so to speak, by the more recent ones. As time passes one of these general qualities, inner clearness and intensity of consciousness, suffers damage. Connections of ideas and series of ideas are subject to the same process of progressive weakening; it is furthered by a resolution of the ideas into their components, as a result of which the now but loosely connected members are eventually united in new combinations. The complete disappearance of the more and more repressed ideas occurs only after a long time. But one should not imagine the repressed ideas in their time of obscuration to be pale images, but rather to be tendencies, "dispositions," to recreate the image contents forced to sink down. If these dispositions are somehow supported and strengthened, it may happen at any one moment that the repressing and hindering ideas become depressed themselves, and that the apparently forgotten idea arises again in perfect clearness.
A third view holds that, at least in the case of complex ideas, obliviscence consists in the crumbling into parts and the loss of separate components instead of in general obscuration. The idea of resolution into component parts recently spoken of supplies here the only explanation. "The image of a complex object is dim in our memory not because as a whole with all its parts present and in order it is illuminated by a feebler light of consciousness, but it is because it has become incomplete. Some parts of it are entirely lacking. Above all the precise connection of those still extant is, in general, missing and is supplied only by the thought that some sort of union once existed between them; the largeness of the sphere in which, without being able to make a final decision, we think this or that connection equally probable, determines the degree of dimness which we are to ascribe to the idea in question."[3]
Each of these opinions receives a certain, but not exclusive, support from the actual inner experiences, or experiences supposed to be actual, which we at times have. And what is the reason? It is that these fortuitous and easily obtained inner experiences are much too vague, superficial and capable of various interpretations to admit in their entirety of only a single interpretation, or even to let it appear as of preponderating probability. Who could, with even tolerable exactness, describe in its gradual course the supposed overlaying or sinking or crumbling of ideas? Who can say anything satisfactory about the inhibitions caused by series of ideas of different extent, or about the disintegration that a firm complex of any kind suffers by the use of its components in new connections? Everybody has his private "explanation" of these processes, but the actual conditions which are to be explained are, after all, equally unknown to all of us.
If one considers the limitation to direct, unaided observation and to the chance occurrence of useful experiences, there seems but little prospect of improvement in conditions. How will one for example determine the degree of obscuration reached at a certain point, or the number of fragments remaining? Or how can the probable course of inner processes be traced if the almost entirely forgotten ideas return no more to consciousness?
Section 27. Methods of Investigation of Actual Conditions
By the help of our method we have a possibility of indirectly approaching the problem just stated in a small and definitely limited sphere, and, by means of keeping aloof for a while from any theory, perhaps of constructing one.
After a definite time, the hidden but yet existent dispositions laid down by the learning of a syllable-series may be strengthened by a further memorisation of the series, and thereby the remaining fragments may be united again to a whole. The work necessary for this compared with that necessary when such dispositions and fragments are absent gives a measure for what has been lost as well as for what remains. The inhibitions which idea-groups of different sorts or extents may occasion in relation to others must, as a result of the interposition of well defined complexes of ideas between learning and relearning, betray itself in the more or less increased work of relearning. The loosening of a bond of connection by some other use of its components can be investigated in a similar manner as follows: after a certain series has been studied, new combinations of the same series are memorised and the change in the amount of work necessary for relearning the original combination is then ascertained.
First, I investigated the first mentioned of these relations and put the question: If syllable series of a definite kind are learned by heart and then left to themselves, how will the process of forgetting go on when left merely to the influence of time or the daily events of life which fill it? The determination of the losses suffered was made in the way described: after certain intervals of time, the series memorised were relearned, and the times necessary in both cases were compared.
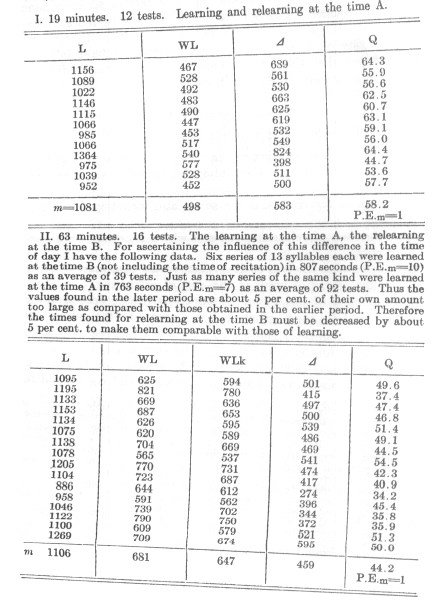
The investigations in question fell in the year 1879-80 and comprised 163 double tests. Each double test consisted in learning eight series of 13 syllables each (with the exception of 38 double tests taken from 11-12 A.M. which contained only six series each) and then in relearning them after a definite time. The learning was continued until two errorless recitations of the series in question were possible. The relearning was carried to the same point; it occurred at one of the following times, -- namely, after about one third of an hour, after 1 hour, after 9 hours, one day, two days, six days, or 31 days.
The times were measured from the completion of the first set of first learnings, as a consequence of which no great accuracy was required in case of the longer intervals. The influence of the last four intervals was tested at three different times of day (p.33 [end of Chapter III]). Some preliminary remarks are necessary before the results obtained can be communicated.
Similar experimental conditions may be taken for granted in the case of the series relearned after a number of whole days. At any rate there is no way of meeting the actual fluctuations even when external conditions are as far as possible similar, other than by a multiplication of the tests. Where the inner dissimilarity was presumably the greatest, namely after the interval of an entire month, I approximately doubled the number of tests.
In the case of an interval of nine hours and an interval of one hour between learning and relearning, there existed, however, a noticeably constant difference in the experimental conditions. In the later hours of the day mental vigor and receptivity are less. The series learned in the morning and then relearned at a later hour, aside from other influences, require more work for relearning than they would if the relearning were done at a time of mental vigor equal to that of the original learning. Therefore, in order to become comparable, the numerical values found for relearning must suffer a diminution which, at least in the case of the 8 hour interval, is so considerable that it cannot be neglected. It must be ascertained how much longer it takes to learn at the time of day, B, series which were learned in a seconds at the time of day, A. The actual determination of this quantity presupposes more tests than I, up to the present, possess. If a necessary but inexact correction is applied to the numbers found for 1 and for 8 hours, these become even more unreliable than if left to themselves.
In the ease of the smallest interval, one third of an hour, the same drawback reappears, though to a less degree; but it is probably compensated for by another circumstance. The interval as a whole is so short that the relearning of the first series of a test followed almost immediately or after an interval of one or two minutes upon the learning of the last series of the same test. For this reason the whole formed so to speak, one continuous test in which the relearning of the series took place under increasingly unfavorable conditions as regards mental freshness. But on the other hand the relearning after such a short interval was done rather quickly. It took hardly half of the time required for the learning. By this means the interval between the learning and relearning of a certain series became gradually smaller. The later series therefore had more favorable conditions with regard to the time interval. In view of the difficulty of more accurate determinations, I have taken it for granted that these two supposed counteracting influences approximately compensated each other.
Section 28. Results
In the following table I denote by:
L the time of first learning of the series in seconds, just as they were found, therefore including the time for the two recitations.
WL the time for relearning the series also including the recitations.
WLk the time of relearning reduced where necessary by a correction.
D
the difference L-WL or L-WLk, as the case may be -- that is, the saving of work in the case of relearning.Q the relation of this saving of work to the time necessary for the first learning, given as a per cent. In the calculation of this quotient I considered only the actual learning time, the time for recitation having been subtracted.[4]
The latter was estimated as being 85 seconds for two recitations of 8 series of 13 syllables each; that would correspond to a duration of 0.41 seconds for each syllable (p. 31 [Chapter III, Section 15]).
Thus Q= (100D )/(L-85)
Finally A, B, C mean the previously mentioned times of day, 10-11A.M., 11-12 A. M., 6-8 P. M.

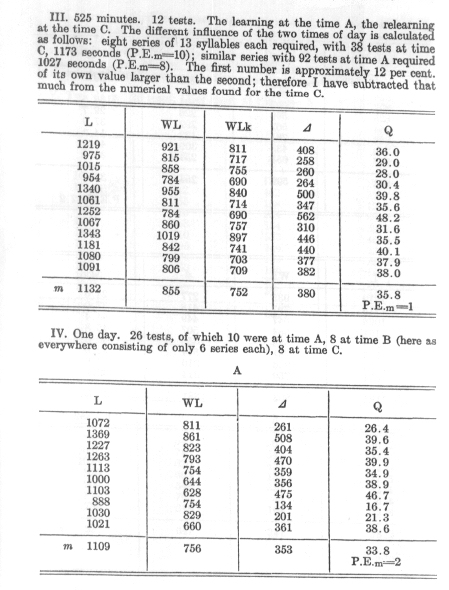
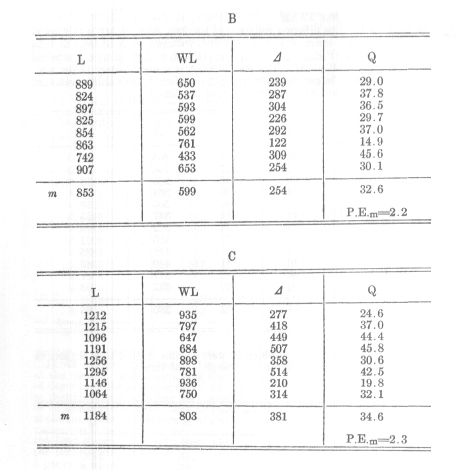

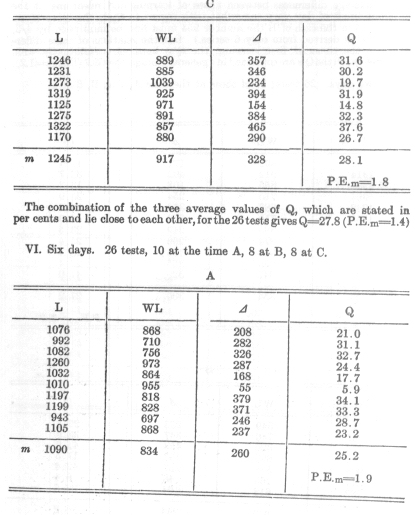
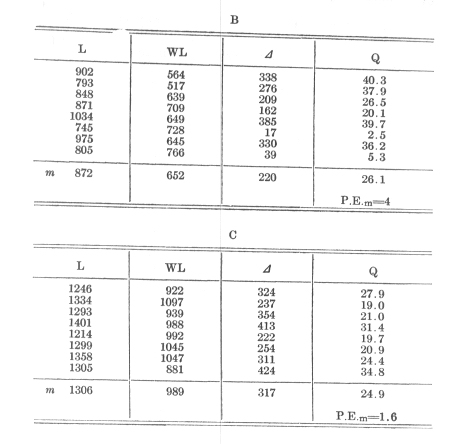

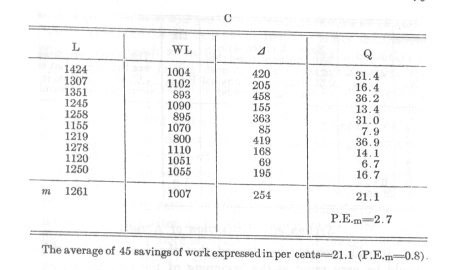
A hasty glance at the figures above reveals the fact that for each interval of time the savings in work which become evident when the series is relearned have very fluctuating values. (This saving in work is each time the measure for the amount remembered at the end of the interval.) This is especially the case with their absolute values (D ), but is also the case with the relative values (Q). The results are taken from the earlier period and suffer from several disturbing influences to which my attention was first drawn by the tests themselves.
In spite of all irregularities in detail, however, they group themselves as a whole with satisfactory certainty into an harmonious picture. As a proof of this the absolute amount of the saving in work is of less value. The latter evidently depends upon the time of day -- i.e., upon the changes in the time of the first learning dependent upon it. When this change is greatest (time C), D also is greatest; for the time B, they are in 3/4 of the cases larger than for the time A (after multiplying by 4/3). On the other hand, the values (Q) found for the relation of each saving of work to the time originally spent, are apparently almost independent of this ratio. Their averages are close together for all three times of day, and do not show any character of increase or decrease in the later hours. Accordingly I here tabulate the latter.
Section 29. Discussion of Results
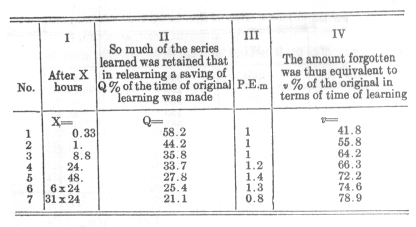
1. It will probably be claimed that the fact that forgetting would be very rapid at the beginning of the process and very slow at the end should have been foreseen. However, it would be just as reasonable to be surprised at this initial rapidity and later slowness as they come to light here under the definite conditions of our experiment for a certain individual, and for a series of 13 syllables. One hour after the end of the learning, the forgetting had already progressed so far that one half the amount of the original work had to be expended before the series could be reproduced again; after 8 hours the work to be made up amounted to two thirds of the first effort. Gradually, however, the process became slower so that even for rather long periods the additional loss could be ascertained only with difficulty. After 24 hours about one third was always remembered; after 6 days about one fourth, and after a whole month fully one fifth of the first work persisted in effect. The decrease of this after-effect in the latter intervals of time is evidently so slow that it is easy to predict that a complete vanishing of the effect of the first memorisation of these series would, if they had been left to themselves, have occurred only after an indefinitely long period of time.
2. Least satisfactory in the results is the difference between the third and fourth values, especially when taken in connection with the greater difference between the fourth and fifth numbers. In the period 9-24 hours the decrease of the after-effect would accordingly have been 2 1/2 per cent. In the period 24 to 48 hours it would have been 6.1 per cent; in the later 24 hours, then, about three times as much as in the earlier 15. Such a condition is not credible, since in the case of all the other numbers the decrease in the after-effect is greatly retarded by an increase in time. It does not become credible even under the plausible assumption that night and sleep, which form a greater part of the 15 hours but a smaller part of the 24, retard considerably the decrease in the after-effect.
Therefore it must be assumed that one of these three values is greatly affected by accidental influences. It would fit in well with the other observations to consider the number 33.7 per cent for the relearning after 24 hours as somewhat too large and to suppose that with a more accurate repetition of the tests it would be 1 to 2 units smaller. However, it is upheld by observations to be stated presently, so that I am in doubt about it.
3. Considering the special, individual, and uncertain character of our numerical results no one will desire at once to know what "law" is revealed in them. However, it is noteworthy that all the seven values which cover intervals of one third of an hour in length to 31 days in length (thus from singlefold to 2,000fold) may with tolerable approximation be put into a rather simple mathematical formula. I call:
t the time in minutes counting from one minute before the en(l of the learning,
b the saving of work evident in relearning, the equivalent of the amount remembered from the first learning expressed in percentage of the time necessary for this first learning,
c and k two constants to be defined presently
Then the following formula may be written:
b = 100k/((log t)c +k)
By using common logarithms and with merely approximate estimates, not involving exact calculation by the method of least squares,
k = 1.84
c = 1.25
Then the results are as follows:
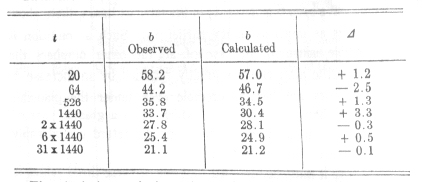
The deviations of the calculated values from the observed values surpass the probable limits of error only at the second and fourth values. With regard to the latter I have already expressed the conjecture that the test might have given here too large a value; the second suffers from an uncertainty concerning the correction made. By the determination made for t, the formula has the advantage that it is valid for the moment in which the learning ceases and that it gives correctly b=100. In the moment when the series can just be recited, the relearning, of course, requires no time, so that the saving is equal to the work expended.
Solving the formula for k we have
k = b(log t)c/(100-b)
This expression, 100-b the complement of the work saved, is nothing other than the work required for relearning, the equivalent of the amount forgotten from the first learning. Calling this, v, the following simple relation results:
b/v = k/(log t)c
To express it in words: when nonsense series of 13 syllables each were memorised and relearned after different intervals, the quotients of the work saved and the work required were about inversely proportional to a small power of the logarithm of those intervals of time. To express it more briefly and less accurately: the quotients of the amounts retained and the amounts forgotten were inversely as the logarithms of the times.
Of course this statement and the formula upon which it rests have here no other value than that of a shorthand statement of the above results which have been found but once and under the circumstances described. Whether they possess a more general significance so that, under other circumstances or with other individuals, they might find expression in other constants I cannot at the present time say.
Section 30. Control Tests
At any rate, even though only for my own case, I can to a certain extent give support to two of the values mentioned by tests which were made at other periods.
From a period even further back than that of the investigations above mentioned I possess several tests with series of ten syllables, fifteen series composing one test. The series were first memorised and then, at an average of 18 minutes after the first learning, each series was relearned. Six tests had the following results:--
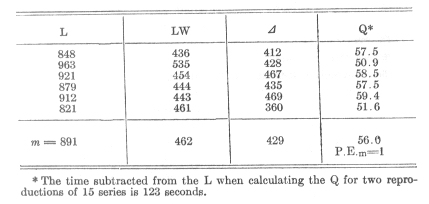
When relearning series of ten syllables each, 18 minutes after the first memorisation, 56 per cent of the work originally expended was therefore saved. The number agrees satisfactorily with the one found above (p. 68 [section 28]) for the relearning of series of syllables of 13 syllables each after 19 minutes, 58 per cent. Also the fact that the latter, notwithstanding the longer interval, is still a little greater, harmonises completely, as will be seen, with the results of the next chapter. According to them, shorter series, when memorised, are forgotten a little more quickly than longer once.
From the period of 1883-84, I have seven tests, consisting of nine series of 12 syllables each that were relearned 24 hours after the first memorisation. The following results were obtained:
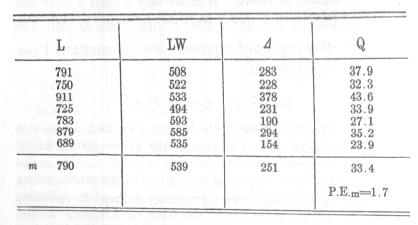
The after-effect of the first memorisation still noticeable after 24 hours, was here equivalent to a saving of work of 33.4 per cent of the first expenditure. This number also agrees satisfactorily with the one communicated above for the relearning of series of 13 syllables each after 24 hours (33.7 per cent), although these two were obtained at far separated time-periods and in the course of widely different investigations.
Footnotes
The curious theory of Bain and others that each idea is lodged in a separate ganglion cell, an hypothesis impossible both psychologically and physiologically, is also rooted to a certain extent in Aristotle's view.
[2] Herbart and his adherents. See, for instance, Waitz, Leehrbuch der Psychologie Sect. 16
[3] Lotze, Metaphysik (1879), p. 521; also Mikrokosoms (3) I, p. 231 ff.