An internet resource developed by
(Return to index)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER II
THE POSSIBILITY OF ENLARGING OUR KNOWLEDGE OF MEMORY
Section 4. The Method of Natural Science
The method of obtaining exact measurements -- i.e., numerically exact ones -- of the inner structure of causal relations is, by virtue of its nature, of general validity. This method, indeed, has been so exclusively used and so fully worked out by the natural sciences that, as a rule, it is defined as something peculiar to them, as the method of natural science. To repeat, however, its 1ogical nature makes it generally applicable to all spheres of existence and phenomena. Moreover, the possibility of defining accurately and exactly the actual behavior of any process whatever, and thereby of giving a reliable basis for the direct comprehension of its connections depends above all upon the possibility of applying this method.
We all know of what this method consists: an attempt is made to keep constant the mass of conditions which have proven themselves causally connected with a certain result; one of these conditions is isolated from the rest and varied in a way that can be numerically described; then the accompanying change on the side of the effect is ascertained by measurement or computation.
Two fundamental and insurmountable difficulties, seem, however, to oppose a transfer of this method to the investigation of the causal relations of mental events in general and of those of memory in particular. In the first place, how are we to keep even approximately constant the bewildering mass of causal conditions which, in so far as they are of mental nature, almost completely elude our control, and which, moreover, are subject to endless and incessant change? In the second place, by what possible means are we to measure numerically the mental processes which filt by so quickly and which on introspection are so hard to analyse? I shall first discuss the second difficulty in connection, of course, with memory, since that is our present concern.
Section 5. Introduction of Numerical Measurements for Memory Contents
If we consider once more the conditions of retention and reproduction mentioned above (sec. 2), but now with regard to the possibility of computation, we shall see that with two of them, at least, a numerical determination and a numerical variation are possible. The different times which elapse between the first production and the reproduction of a series of ideas can be measured and the repetitions necessary to make these series reproducible can be counted. At first sight, however, there seems to be nothing similar to this on the side of the effects. Here there is only one alternative, a reproduction is either possible or it is not possible. It takes place or it does not take place. Of course we take for granted that it may approach, under different conditions, more or less near to actual occurrence so that in its subliminal existence the series possesses graded differences. But as long as we limit our observations to that which, either by chance or at the call of our will, comes out from this inner realm, all these differences are for us equally non-existent.
By somewhat less dependence upon introspection we can, however, by indirect means force these difference into the open. A poem is learned by heart and then not again repeated. We will suppose that after a half year it has been forgotten: no effort of recollection is able to call it back again into consciousness. At best only isolated fragments return. Suppose that the poem is again learned by heart. It then becomes evident that, although to all appearances totally forgotten, it still in a certain sense exists and in a way to be effective. The second learning requires noticeably less time or a noticeably smaller number of repetitions than the first. It also requires less time or repetitions than would now be necessary to learn a similar poem of the same length. In this difference in time and number of repetitions we have evidently obtained a certain measure for that inner energy which a half year after the first learning still dwells in that orderly complex of ideas which make up the poem. After a shorter time we should expect to find the difference greater; after a longer time we should expect to find it less. If the first committing to memory is a very careful and long continued one, the difference will be greater than if it is desultory and soon abandoned.
In short, we have without doubt in these differences numerical expressions for the difference between these subliminally persistent series of ideas, differences which otherwise we would have to take for granted and would not be able to demonstrate by direct observation. Therewith we have gained possession of something that is at least like that which we are seeking in our attempt to get a foothold for the application of the method of the natural sciences: namely, phenomena on the side of the effects which are clearly ascertainable, which vary in accordance with the variation of conditions, and which are capable of numerical determination. Whether we possess in them correct measures for these inner differences, and whether we can achieve through them correct conceptions as to the causal relations into which this hidden mental life enters -- these questions cannot be answered a priori. Chemistry is just as little able to determine a priori whether it is the electrical phenomena, or the thermal, or some other accompaniment of the process of chemical union, which gives it its correct measure of the effective forces of chemical affinity. There is only one way to do this, and that is to see whether it is possible to obtain, on the presupposition of the correctness of such an hypothesis, well classified, uncontradictory results, and correct anticipations of the future.
Instead of the simple phenomenon -- occurrence or non-occurrence of a reproduction -- which admits of no numerical distinction, I intend therefore to consider from the experimental standpoint a more complicated process as the effect, and I shall observe and measure its changes as the conditions are varied. By this I mean the artificial bringing about by an appropriate number of repetitions of a reproduction which would not occur of its own accord.
But in order to realise this experimentally, two conditions at least must be fulfilled.
In the first place, it must be possible to define with some certainty the moment when the goal is reached -- i.e., when the process of learning by heart is completed. For if the process of learning by heart is sometimes carried past that moment and sometimes broken off before it, then part of the differences found under the varying circumstances would be due to this inequality, and it would be incorrect to attribute it solely to inner differences in the series of ideas. Consequently among the different reproductions of, say, a poem, occurring during the process of its memorisation, the experimenter must single out one as especially characteristic, and be able to find it again with practical accuracy.
In the second place the presupposition must be allowed that the number of repetitions by means of which, the other conditions being unchanged, this characteristic reproduction is brought about would be every time the same. For if this number, under conditions otherwise equivalent, is now this and now that, the differences arising from varied conditions lose, of course, all significance for the critical evaluation of those varying conditions.
Now, as far as the first condition is concerned, it is easily fulfilled wherever you have what may properly be called learning by heart, as in the case of poems, series of words, tone-sequences, and the like. Here, in general, as the number of repetitions increases, reproduction is at first fragmentary and halting; then it gains in certainty; and finally takes place smoothly and without error. The first reproduction in which this last result appears can not only be singled out as especially characteristic, but can also be practically recognised. For convenience I will designate this briefly as the first possible reproduction.
The question now is: -- Does this fulfill the second condition mentioned above? Is the number of repetitions necessary to bring about this reproduction always the same, the other conditions being equivalent?
However, in this form, the question will be justly rejected because it forces upon us, as if it were an evident supposition, the real point in question, the very heart of the matter, and admits of none but a misleading answer. Anyone will be ready to admit without hesitation that this relation of dependence will be the same if perfect equality of experimental condition is maintained. The much invoked freedom of the will, at least, has hardly ever been misunderstood by anybody so far as to come in here. But this theoretical constancy is of little value: How shall I find it when the circumstances under which I am actually forced to make my observations are never the same? So I must rather ask :-- Can I bring under my control the inevitably and ever fluctuating circumstances and equalise them to such an extent that the constancy presumably existent in the causal relations in question becomes visible and palpable to me?
Thus the discussion of the one difficulty which opposes an exact examination of the causal relations in the mental sphere has led us of itself to the other (sec. 4). A numerical determination of the interdependent changes of cause and effect appears indeed possible if only we can realise the necessary uniformity of the significant conditions in the repetition of our experiments.
Section 6. The Possibility of Maintaining the Constancy of Conditions Requisite for Research
He who considers the complicated processes of the higher mental life or who is occupied with the still more complicated phenomena of the state and of society will in general be inclined to deny the possibility of keeping constant the conditions for psychological experimentation. Nothing is more familiar to us than the capriciousness of mental life which brings to nought all foresight and calculation. Factors which are to the highest degree determinative and to the same extent changeable, such as mental vigor, interest in the subject, concentration of attention, changes in the course of thought which have been brought about by sudden fancies and resolves -- all these are either not at all under our control or are so only to an unsatisfactory extent.
However, care must be taken not to ascribe too much weight to these views, correct in themselves, when dealing with fields other than those of the processes by the observation of which these views were obtained. All such unruly factors are of the greatest importance for higher mental processes which occur only by an especially favorable concurrence of circumstances. The more lowly, commonplace, and constantly occurring processes are not in the least withdrawn from their influence, but we have it for the most part in our power, when it is a matter of consequence, to make this influence only slightly disturbing. Sensorial perception, for example, certainly occurs with greater or less accuracy according to the degree of interest; it is constantly given other directions by the change of external stimuli and by ideas. But, in spite of that, we are on the whole sufficiently able to see a house just when we want to see it and to receive practically the same picture of it ten times in succession in case no objective change has occurred.
There is nothing a priori absurd in the assumption that ordinary retention and reproduction, which, according to general agreement, is ranked next to sensorial perception, should also behave like it in this respect. Whether this is actually the case or not, however, I say now as I said before, cannot be decided in advance. Our present knowledge is much too fragmentary, too general, too largely obtained from the extraordinary to enable us to reach a decision on this point by its aid; that must be reserved for experiments especially adapted to that purpose. We must try in experimental fashion to keep as constant as possible those circumstances whose influence on retention and reproduction is known or suspected, and then ascertain whether that is sufficient. The material must be so chosen that decided differences of interest are, at least to all appearances, excluded; equality of attention may be promoted by preventing external disturbances; sudden fancies are not subject to control, but, on the whole, their disturbing effect is limited to the moment, and will be of comparatively little account if the time of the experiment is extended, etc.
When, however, we have actually obtained in such manner the greatest possible constancy of conditions attainable by us, how are we to know whether this is sufficient for our purpose? When are the circumstances, which will certainly offer differences enough to keen observation, sufficient1y constant? The answer may be made: -- When upon repetition of the experiment the results remain constant. The latter statement seems simple enough to be self-evident, but on closer approach to the matter still another difficulty is encountered.
Section 7. Constant Averages
When shall the results obtained from repeated experiments under circumstances as much alike as possible pass for constant or sufficiently constant? Is it when one result has the same value as the other or at least deviates so little from it that the difference in proportion to its own quantity and for our purposes is of no account?
Evidently not. That would be asking too much, and is not necessarily obtained even by the natural sciences. Then, perhaps it is when the averages from larger groups of experiments exhibit the characteristics mentioned above?
Again evidently not. That would be asking too little. For, if observation of processes that resemble each other from any point of view are thrown together in sufficiently large numbers, fairly constant mean values are almost everywhere obtained which, nevertheless, possess little or no importance for the purposes which we have here. The exact distance of two signal poles, the position of a star at a certain hour, the expansion of a metal for a certain increase of temperature, all the numerous coefficients and other constants of physics and chemistry are given us as average values which only approximate to a high degree of constancy. On the other hand the number of suicides in a certain month, the average length of life in a given place, the number of teams and pedestrians per day at a certain street corner, and the like, are also noticeably constant, each being an average from large groups of observations. But both kinds of numbers, which I shall temporarily denote as constants of natural science and statistical constants, are, as everybody knows, constant from different causes and with entirely different significance for the knowledge of causal relations.
These differences can be formulated as follows: --
In the case of the constants of the natural sciences each individual effect is produced by a combination of causes exactly alike. The individual values come out somewhat differently because a certain number of those causes do not always join the combination with exactly the same values (e.g., there are little errors in the adjustment and reading of the instruments, irregularities in the texture or composition of the material examined or employed, etc.). However, experience teaches us that this fluctuation of separate causes does not occur absolutely irregularly but that as a rule it runs through or, rather, tries out limited and comparatively small circles of values symmetrically distributed around a central value. If several cases are brought together the effects of the separate deviations must more
and more compensate each other and thereby be swallowed up in the central value around which they occur. And the final result of combining the values will be approximately the same as if the actually changeable causes had remained the same not only conceptually but also numerically. Thus, the average value is in these cases the adequate numerical representative of a conceptually definite and well limited system of causal connections; if one part of the system is varied, the accompanying changes of the average value again give the correct measure for the effect of those deviations on the total complex.
On the other hand, no matter from what point of view statistical constants may be considered it cannot be said of them that each separate value has resulted from the combination of causes which by themselves had fluctuated within tolerably narrow limits and in symmetrical fashion. The separate effects arise, rather, from an oftimes inextricable multiplicity of causal combinations of very different sorts, which, to be sure, may share numerous factors with each other, but which, taken as a whole, have no conceivable community and actually correspond only in some one characteristic of the effects. That the value of the separate factors must be very different is, so to say, self evident. That, nevertheless, approximately constant values appear even here by the combining of large groups -- this fact we may make intelligible by saying that in equal and tolerably large intervals of time or extents of space the separate causal combinations will be realised with approximately equal frequency; we do this without doing more than to acknowledge as extant a peculiar and marvellous arrangement of nature. Accordingly these constant mean values represent no definite and separate causal systems but combinations of such which are by no means of themselves transparent. Therefore their changes upon variation of conditions afford no genuine measure of the effects of these variations but only indications of them. They are of no direct value for the setting up of numerically exact relations of dependence but they are preparatory to this.
Let us now turn back to the question raised at the beginning of this section. When may we consider that this equality of conditions which we have striven to realise experimentally has been attained? The answer runs as follows: When the average values of several observations are approximately constant and when at the same time we may assume that the separate cases belong to the same causal system, whose elements, however, are not limited to exclusively constant values, but may run through small circles of numerical values symmetrical around a middle value.
Section 8. The Law of Errors
Our question, however, is not answered conclusively by the statement just made. Suppose we had in some way found satisfactorily constant mean values for some psychical process, how would we go about it to learn whether we might or might not assume a homogeneous causal condition, necessary for their further utilisation? The physical scientist generally knows beforehand that he will have to deal with a single causal combination, the statistician knows that he has to deal with a mass of them, ever inextricable despite all analysis. Both know this from the elementary knowledge they already possess of the nature of the processes before they proceed with the more detailed investigations. Just as, a moment ago, the present knowledge of psychology appeared to us too vague and unreliable to be depended upon for decision about the possibility of constant experimental conditions; so now it may prove insufficient to determine satisfactorily whether in a given case we have to deal with a homogeneous causal combination or a manifold of them which chance to operate together. The question is, therefore, whether we may throw light on the nature of the causation of the results we obtain under conditions as uniform as possible by the help of some other criterion.
The answer must be: This cannot be done with absolute certainty, but can, nevertheless, be done with great probability. Thus, a start has been made from presuppositions as similar as possible to those by which physical constants have been obtained and the consequences which flow from them have been investigated. This has been done for the distribution of the single values about the resulting central value and quite independently of the actual concrete characteristics of the causes. Repeated comparisons of these calculated values with actual observations have shown that the similarity of the suppositions is indeed great enough to 1ead to an agreement of the result. The outcome of these speculations closely approximates to reality. It consists in this, -- that the grouping of a large number of separate values that have arisen from causes of the same kind and with the modifications repeatedly mentioned, may be correctly represented by a mathematical formula, the so-called Law of Errors. This is especially characterised by the fact that it contains but one unknown quantity. This unknown quantity measures the relative compactness of the distribution of the separate values around their central tendency. It therefore changes according to the kind of observation and is determined by calculation from the separate values.
NOTE. For further information concerning this formula, which is not here our concern, I must refer to the text-books on the calculation of probabilities and on the theory of errors. For readers unfamiliar with the latter a graphic explanation will be more comprehensible than a statement and discussion of the formula. Imagine a certain observation to be repeated 1,000 times. Each observation as such is represented by a space of one square millimeter, and its numerical value, or rather its deviation from the central value of the whole 1,000 observations, by its position on the horizontal line p q of the adjoining Figure 1.
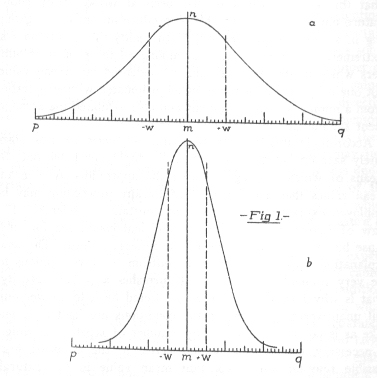
For every observation which exactly corresponds with the central value one square millimeter is laid off on the vertical line m n. For each observed value which deviates by one unit from the central value upward one square millimeter is laid off on a vertical line to right of m n and distant one millimeter from it, etc. For every observed value which deviates by x units above (or below) the central value, one sq. mm. is placed on a vertical line distant from m n by x mms., to the right (or left, for values below the central value). When all the observations are arranged in this way the outer contour of the figure may be so compacted that the projecting corners of the separate squares are transformed into a symmetrical curve. If now the separate measures are of such a sort that their central value may be considered as a constant as conceived by physical science, the form of the resulting curve is of the kind marked a and b in Fig. 1. If the middle value is a statistical constant, the curve may have any sort of a form. (The curves a and b with the lines p q include in each case an area of 1,000 sq. mms. This is strictly the case only with indefinite prolongation of the curves and the lines p q, but these lines and curves finally approach each other so closely that where the drawing breaks off only two or three sq. mms. at each end of the curve are missing from the full number. Whether, for a certain group of observations, the curve has a more steep or more flat form depends on the nature of those observations. The more exact they are, the more will they pile up around the central value; and the more infrequent the large deviations, the steeper will the curve be and vice versa. For the rest the law of formation of the curve is always the same. Therefore, if a person, in the case of any specific combination of observations, obtains any measure of the compactness of distribution of the observations, he can survey the grouping of the whole mass. He could state, for instance, how often a deviation of a certain value occurs and how many deviations fall between certain limits. Or -- as I shall show in what follows -- he may state what amount of variation includes between itself and the central value a certain per cent of all the observed values. The lines +w and -w of our figure, for instance, cut out exactly the central half of the total space representing the observations. But in the case of the more exact observations of 1b they are only one half as far from m n as in 1a. So the statement of their relative distances gives also a measure of the accuracy of the observations.
Therefore, it may be said: wherever a group of effects may be considered as having originated each time from the same causal combination, which was subject each time only to so-called accidental disturbances, then these values arrange themselves in accordance with the "law of errors."
However, the reverse of this proposition is not necessarily true, namely, that wherever a distribution of values occurs according to the law of errors the inference may be drawn that this kind of causation has been at work. Why should nature not occasionally be able to produce an analogous grouping in a more complicated way? In reality this seems only an extremely rare occurrence. For among all the groups of numbers which in statistics are usually condensed into mean values not one has as yet been found which originated without question from a number of causal systems and also exhibited the arrangement summarised by the "law of errors."[1]
Accordingly, this law may be used as a criterion, not an absolutely safe one to be sure, but still a highly probable one, by means of which to judge whether the approximately constant mean values that may be obtained by any proceeding may be employed experimentally as genuine constants of science. The Law of Errors does not furnish sufficient conditions for such a use but it does furnish one of the necessary ones. The final explanation must depend upon the outcome of investigations to the very foundations of which it furnishes a certain security. That is why I applied the measure offered by it to answer our still unanswered question: If the conditions are kept as much alike as is possible, is the average number of repetitions, which is necessary for learning similar series to the point of first possible reproduction, a constant mean value in the natural science sense? And I may anticipate by saying that in the case investigated the answer has come out in the affirmative.
Section 9. Resumé
Two fundamental difficulties arise in the way of the application of the so-called Natural Science Method to the examination of psychical processes:
(1) The constant flux and caprice of mental events do not admit of the establishment of stable experimental conditions.
(2) Psychical processes offer no means for measurement or enumeration.
In the case of the special field of memory (learning, retention, reproduction) the second difficulty may be overcome to a certain extent. Among the external conditions of these processes some are directly accessible to measurement (the time, the number of repetitions). They may be employed in getting numerical values indirectly where that would not have been possible directly. We must not wait until the series of ideas committed to memory return to consciousness of themselves, but we must meet them halfway and renew them to such an extent that they may just be reproduced without error. The work requisite for this under certain conditions I take experimentally as a measure of the influence of these conditions; the differences in the work which appear with a change of conditions I interpret as a measure of the influence of that change.
Whether the first difficulty, the establishment of stable experimental conditions, may also be overcome satisfactorily cannot be decided a priori. Experiments must be made under conditions as far as possible the same, to see whether the results, which will probably deviate from one another when taken separately, will furnish constant mean values when collected to form larger groups. However, taken by itself, this is not sufficient to enable us to utilise such numerical results for the establishment of numerical relations of dependence in the natural science sense. Statistics is concerned with a great mass of constant mean values that do not at all arise from the frequent repetition of an ideally frequent occurrence and therefore cannot favor further insight into it. Such is the great complexity of our mental life that it is not possible to deny that constant mean values, when obtained, are of the nature of such statistical constants. To test that, I examine the distribution of the separate numbers represented in an average value. If it corresponds to the distribution found everywhere in natural science, where repeated observation of the same occurrence furnishes different separate values, I suppose -- tentatively again -- that the repeatedly examined psychical process in question occurred each time under conditions sufficiently similar for our purposes. This supposition is not compulsory, but is very probable. If it is wrong, the continuation of experimentation will presumably teach this by itself: the questions put from different points of view will lead to contradictory results.
Section 10. The Probable Error
The quantity which measures the compactness of the observed values obtained in any given case and which makes the formula which represents their distribution a definite one may, as has already been stated, be chosen differently. I use the so-called "probable error" (P.E.) -- i.e., that deviation above and below the mean value which is just as often exceeded by the separate values as not reached by them, and which, therefore, between its positive and negative limits, includes just half of all the observational results symmetrically arranged around the mean value. As is evident from the definition these values can be obtained from the results by simple enumeration; it is done more accurately by a theoretically based calculation.
If now this calculation is tried out tentatively for any group of observations, a grouping of these values according to the "law of errors" is recognised by the fact that between the sub-multiples and the multiples of the empirically calculated probable error there are obtained as many separate measures symmetrically arranged about a central value as the theory requires.
According to this out of 1,000 observations there should be:
|
Within the limits |
Number of separate measures |
|
± 1/10 P.E. |
54 |
|
± 1/6 P.E. |
89.5 |
|
± 1/4 P.E. |
134 |
|
± 1/2 P.E. |
264 |
|
± [sic] P.E. |
500 |
|
± 1 1/2 P.E. |
688 |
|
± 2 P.E. |
823 |
|
± 2 1/2 P.E. |
908 |
|
± 3 P.E. |
957 |
|
± 4 P.E. |
993 |
If this conformity exists in a sufficient degree, then the mere statement of the probable error suffices to characterise the arrangement of all the observed values, and at the same time its quantity gives a serviceable measure for the compactness of the distribution around the central value-i.e., for its exactness and trustworthiness.
As we have spoken of the probable error of the separate observations, (P.E.o), so can we also speak of the probable error of the measures of the central tendency, or mean values, (P.E.m). This describes in similar fashion the grouping which would arise for the separate mean values if the observation of the same phenomenon were repeated very many times and each time an equally great number of observations were combined into a central value. It furnishes a brief but sufficient characterisation of the fluctuations of the mean values resulting from repeated observations, and along with it a measure of the security and the trustworthiness of the results already found.
The P.E.m is accordingly in general included in what follows. How it is found by calculation, again, cannot be explained here; suffice it that what it means be clear. It tells us, then, that, on the basis of the character of the total observations from which a mean value has just been obtained, it may be expected with a probability of 1 to 1 [sic] that the latter value departs from the presumably correct average by not more at the most than the amount of its probable error. By the presumably correct average we mean that one which would have been obtained if the observations had been indefinitely repeated. A larger deviation than this becomes improbable in the mathematical sense -- i.e., there is a greater probability against it than for it. And, as a glance at the accompanying table shows us, the improbability of larger deviations increases with extreme rapidity as their size increases. The probability that the obtained average should deviate from the true one by more than 2 1/2 times the probable error is only 92 to 908, therefore about 1/10; the probability for its exceeding four times the probable error is very slight, 7 to 993 (1 to 142).
Footnotes