Classics in the History of Psychology
An internet resource developed by
Christopher D. Green
York University, Toronto, Ontario
(Return to Classics index)
[Classics Editor's Note: Footnotes are in square brackets; references in round brackets]
On the Perception of Incongruity: A Paradigm
Jerome S. Bruner and Leo Postman (1949)
First published in Journal of Personality, 18, 206-223.
Perceiving, for all its nicety of functioning in the dark room under strict instructions for accuracy, comprises a highly complex series of little understood psychological processes. For under all conditions, perceiving represents a resultant of two complex sets of specifications. One set describes the conditions of stimulation. This is done either in terms of physical measures such as wave length, or in terms of psychological norms such as in the description of a picture as that picture is seen by "normal" observers under optimal conditions and with a set for accuracy. This first set of specifications we are used to calling "stimulus" factors.
Stimuli, however, do not act upon an indifferent organism. There is never, in the old-fashioned language of G. F. Stout, anoetic sentience. The organism in perception is in one way or another in a state of expectancy about the environment. It is a truism worth repeating that the perceptual effect of a stimulus is necessarily dependent upon the set or expectancy of the organism. And so, in many situations the student of perception must also specify the expectancies of the organism when exposed to stimulation. If we sometimes, in simple sensory experiments, fail to do so, the reason is not that we do not care about the attitude of the organism but, rather, that we take it for granted that the observer is attentive to the task and that he is seeking to judge in terms of some required sensory dimension and not some other.
There have been very few systematic efforts to analyze the dimensions of set and to formulate laws regarding the effectiveness of set in perception such as those which describe stimulus-perception relationships. That students of nonsensory or "directive" factors in perception have thus far refrained from any large-scale statement of principles, while it is a mark of admirable modesty in the face of a very confusing array of experimental data, is highly regrettable. [p. 207] For it has prevented the emergence of new hypotheses which, flowing even from premature principles, might serve to test the utility of theories of perception.
The present study, though empirical in nature, is essentially an essay in the theory of perception -- or at least that part of the theory of perception which deals with directive factors in the perceiving process. Our basic axiom has already been stated -- that perceiving is a process which results from the stimulation of a prepared or eingestellt organism. A second axiom concerns the operation of such directive factors: given a stimulus input of certain characteristics, directive processes in the organism operate to organize the perceptual field in such a way as to maximize percepts relevant to current needs and expectations and to minimize percepts inimical to such needs and expectations. This "minimax" axiom we have referred to elsewhere as the construction-defense balance in perceiving (1).
All of which is not to say that perception is always wishful or "autistic." Indeed, that is not the point. "Wishfulness" has to do with the nature of the expectations which are at work and is not a term relevant to the perceiving process as such. By "wishful" we mean an expectation with a low probability of being confirmed by events. The construction-defense process operates where expectations are "realistic" or where they are "wishful." In the former case, it is simply a matter of "constructing" a percept which is relevant, say, to the exigencies of locomotion, "defending" against percepts which, though potentially wish-fulfilling, are disruptive to the task of locomotion. While directive factors do operate in the interests of locomotion, the skier on the trail does not organize the distant steep hillside in a manner which would make his own path seem less steep and hazardous. Rather, in his perception, the dangers ahead may be sharpened and emphasized. Similarly, although it is the other side of the coin of "realism," one smitten by love does rather poorly in perceiving the linear characteristics of his beloved. His perceptual expectancies, so to speak, are elsewhere. The construction-defense balance operates along other lines. One sees softness of the skin, loftiness of brow, lightness of step -- but perception of certain physical flaws does not materialize.
[p. 208] Perceptual expectancies, whether realistic or wishful, continue to operate so long as they are reinforced by the outcome of events. In short, expectancies continue to mold perceptual organization in a self-sustaining fashion so long as they are confirmed. It is when well-established expectancies fail of confirmation that the organism may face a task of perceptual reorganization.
The principal concern of this paper is with the perceptual events which occur when perceptual expectancies fail of confirmation -- the problem of incongruity. Incongruity represents a crucial problem for a theory of perception because, by its very nature, its perception represents a violation of expectation. An unexpected concatenation of events, a conspicuous mismatching, an unlikely pairing of cause and effect -- all of these have in common a violation of normal expectancy. Yet incongruities are perceived. Through a process of trial-and-check, to borrow a phrase from Professor Woodworth (8), the organism operates to discover whether any given expectancy will "pay off." It is either a very sick organism, an overly motivated one, or one deprived of the opportunity to "try-and-check" which will not give up an expectancy in the face of a contradicting environment.
It would be our contention, nonetheless, that for as long as possible and by whatever means available, the organism will ward off the perception of the unexpected, those things which do not fit his prevailing set. Our assumption, and it is hardly extravagant, is simply that most people come to depend upon a certain constancy in their environment and, save under special conditions, attempt to ward off variations from this state of affairs: "Thar ain't no such animal," the hayseed is reputed to have said on seeing his first giraffe.
Turning now to the specific study to be reported, our aim was to observe the behavior of intact, normal organisms faced with incongruous situations. How are such situations coped with perceptually? What is seen and under what conditions? We shall not be concerned with factors making for differences among individuals in their "tolerance for incongruity." Such studies are now being planned. It is essential first to examine how incongruity is dealt with, what repertory of responses is available to the organism in incongruous situations.
[p. 209]The Experiment
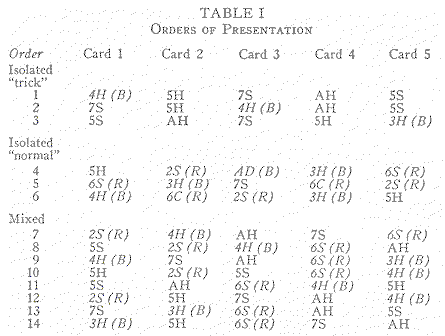
Twenty-eight subjects, students at Harvard and Radcliffe, were shown successively by tachistoscopic exposure five different playing cards. From one to four of these cards were incongruous -- color and suit were reversed. Order of presentation of normal and incongruous cards was randomized. The normal and "trick" cards used were the following.
Normal cards (printed in their proper color): five of hearts, ace of hearts, five of spades, seven of spades.
Trick cards (printed with color reversed): three of hearts (black), four of hearts (black), two of spades (red), six of spades (red), ace of diamonds (black), six of clubs (red).
Fourteen orders of presentation were worked out, and two subjects were presented the cards in each of these orders. There were three types of stimulus series: (1) a single trick card embedded in a series of four normal cards; (2) a single normal card embedded in a series of four trick cards; (3) mixed series in which trick and normal cards were in the ratio of 3:2 or 2:3. A summary of the orders of presentation appears in Table 1.

The reader will note that the average number value of the trick cards is slightly under 4 (3.94) and slightly over 4 for the normal cards (4.35) -- a flaw [p. 210] which operates slightly against the recognition of normal cards since lower value cards are probably more easily recognized.
Each card was presented successively until correct recognition occurred, three times each at 10 ms., 30 ms., 50 ms., 70 ms., 100ms., 150 ms., 200 ms., 250 ms., 300 ms., 400 ms., 450 ms., 500 ms., and then in steps of 100 ms. to 1000 ms. If at 1000 ms. recognition did not occur, the next card was presented. In determining thresholds, correct recognition was defined as two successive correct responses. At each exposure, the subject was asked to report everything he saw or thought he saw.
The cards were mounted on medium gray cardboard and were shown in a Dodge-Gerbrands tachistoscope. The pre-exposure field was of the same gray color and consistency as the exposure field save that it contained no playing card. The light in the tachistoscope was provided by two G. E. daylight fluorescent tubes.
A word about the color of the incongruous cards is in order. Our efforts to have them printed by a playing card company were in vain. We therefore used poster paints to alter the colors of the cards. We had difficulty matching the red of a playing card, our best match being a slightly muddier and less yellow red than that of a regular card. Because of this, all red cards -- trick and normal alike -- were painted over in this color.
Results
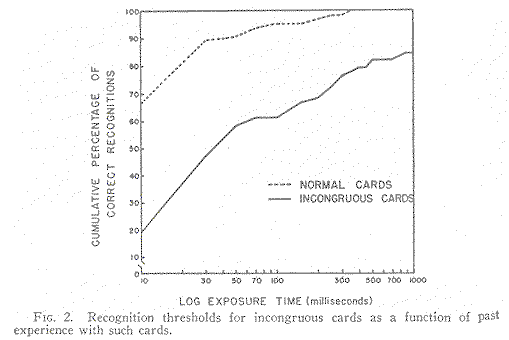
Thresholds. Perhaps the most central finding is that the recognition threshold for the incongruous playing cards (whose with suit and color reversed) is significantly higher than the threshold for normal cards. While normal cards on the average were recognized correctly -- here defined as a correct response followed by a second correct response -- at 28 milliseconds, the incongruous cards required 114 milliseconds. The difference, representing a fourfold increase in threshold, is highly significant statistically, t being 3.76 (confidence level < .01).
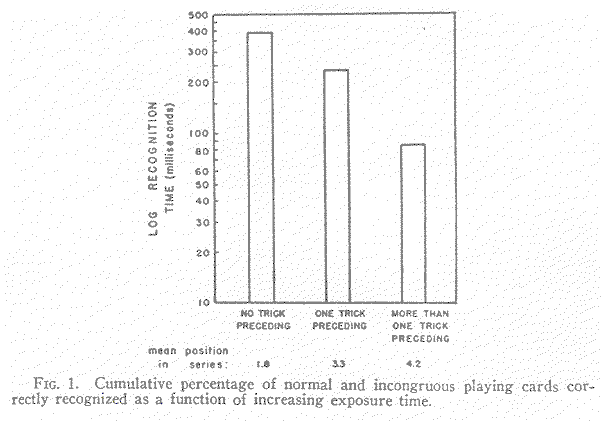
The threshold data, expressed as the cumulative percentage of stimuli correctly recognized as a function of increasing exposure time, are presented in Figure 1. The curves, generally, are parallel. The reader will note that even at the longest exposure used, 1000 ms., only 89.7 per cent of the incongruous cards had been correctly [p. 211] recognized, while 100 per cent of the normal cards had been recognized by 350 milliseconds.
Our design was such that we might test the hypothesis that the more experience a subject had had in the past with incongruity, the less difficulty would he have in recognizing incongruity of a related nature. Indeed, this is tantamount to saying that when one has experienced an incongruity often enough, it ceases to violate expectancy and hence ceases to be incongruous.
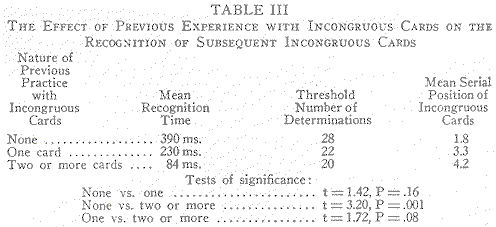
Experience with an incongruity is effective in so far as it modifies the set of the subject to prepare him for incongruity. To take an example, the threshold recognition time for incongruous cards presented before the subject has had anything else in the tachistoscope -- normal or incongruous -- is 360 milliseconds. If he has had experience in the recognition of one or more normal cards before being presented an incongruous stimulus, the threshold rises slightly but insignificantly to 420 milliseconds. Prior experience with normal cards does not lead to better recognition performance with incongruous cards (Table II). If, however, an observer has had to recognize one incongruous card, the threshold for the next trick card he is presented drops to 230 milliseconds. And if, finally, the incongruous card comes after experience with two or three previously exposed trick cards, threshold [p. 212] drops still further to 84 milliseconds. These figures, along with relevant tests of significance are summarized in Table III and plotted in Figure 2.

[p. 213] The point immediately arises as to how much the decrease in threshold noted above is due to sheer number of trials in the tachistoscope (skill practice) and how much to the heightened expectancy of incongruity. Unfortunately our data are confounded in a complicated way here, and we shall have to depend upon rather broad inferences. We cannot partial out the differential effect of serial position of a card, whether first or third or fifth in the series independently of the kinds of experience the subject had before being presented any given card. Because of the nature of our design, such a procedure would leave us with groups differing in number and in the difficulty of cards presented. What evidence we have points, however, to the importance of previous experience with incongruity quite apart from skill practice. We have remarked already that previous tachistoscopic experience with normal cards serves to raise slightly the threshold for incongruous cards. Sheer skill practice cannot, then, be solely or even largely responsible for decreasing the threshold for incongruous cards.
Reactions to incongruity. We may ask properly at this point why the recognition threshold for incongruous stimuli was four times as high as the threshold for normal cards. The answer, it appears from an analysis of the data, lies in the manner in which subjects dealt with or coped with incongruity per se.
Generally speaking, there appear to be four kinds of reaction to rapidly presented incongruities. The first of these we have called the dominance reaction. It consists, essentially, of a "perceptual denial" of the incongruous elements in the stimulus pattern. Faced with a red six of spades, for example, a subject may report with considerable assurance, "the six of spades" or the "six of hearts," depending upon whether he is color or form bound (vide infra). In the one case the form dominates and the color is assimilated to it; in the other the stimulus color dominates and form is assimilated to it. In both instances the perceptual resultant conforms with past expectations about the "normal" nature of playing cards.
A second technique of dealing with incongruous stimuli we have called compromise. In the language of Egon Brunswik (2), it is the perception of a Zwischengegenstand or compromise object which composes the potential conflict between two or more perceptual in- [p. 214] tentions. Three examples of color compromise: (a) the red six of spades is reported as either the purple six of hearts or the purple six of spades; (b) the black four of hearts is reported as a "grayish" four of spades; (c) the red six of clubs is seen as "the six of clubs illuminated by red light."
A third reaction may be called disruption. A subject fails to achieve a perceptual organization at the level of coherence normally attained by him at a given exposure level. Disruption usually follows upon a period in which the subject has failed to resolve the stimulus in terms of his available perceptual expectations. He has failed to confirm any of his repertory of expectancies. Its expression tends to be somewhat bizarre: "I don't know what the hell it is now, not even for sure whether it's a playing card," said one frustrated subject after an exposure well above his normal threshold.
Finally, there is recognition of incongruity, the fourth, and viewed from the experimenter's chair, most successful reaction. It too is marked by some interesting psychological by-products, of which more in the proper place.
Consider now each of these four reactions, the forms they take, and the way in which they differentiate responses to normal and trick cards.
Dominance Reactions
A first datum is that 27 out of our 28 subjects showed dominance responses to the trick cards in their records, some considerably more than others. Strictly speaking, there is often no determinate way of discovering dominance relations to a normal card. A correct response may be a dominance response -- either dominance of color or dominance of form. A few instances of discernible dominance reactions to the normal cards were observed in the case of erroneous perceptions. There were, for example, instances in which a red normal card was seen as black and form was assimilated to match the black color. One subject saw the red five of hearts as the black five of spades for 8 out of the 25 exposures required for full recognition; another saw the red ace of hearts as the black ace of clubs for 3 out of 15 trials required for recognition. In sum, then, 7 per cent of the subjects showed dominance responses to the normal cards -- attempting to rectify an incongruity imposed on them- [p. 215] selves by seeing our imperfect red cards as black -- while 96 per cent of the subjects showed dominance reactions to the incongruous cards.
The nature of the dominance reactions to the trick cards is easily described. First, such reactions occurred with equal frequency to trick black and trick red cards. Two options were available: either the subject could organize the field in terms of suit, e.g., hearts seen as red regardless of their stimulus color; or the field could be organized in terms of color, e.g., a red card seen as a heart or diamond regardless of its true suit.
It must be said, with whatever bearing it may have for Rorschach theory, that subjects showed a marked preference for one or another of the dominance options. Assuming that a fifty-fifty distribution of form-and color-dominant responses would be expected by chance, we tested for form and color types among our subjects. Of the 27 subjects showing dominance responses, 19 showed preferences for form or color in excess of chance at the .05 level or better; the remaining 8 being equally prone to both kinds of response.
To sum up, dominance reactions to trick cards were almost universal among our subjects. An incongruous stimulus was rendered congruent with expectancy by the operation of either form or color dominance. Only a small fraction of the responses to the normal cards was of this type; and where such responses occurred, they were always elicited by incongruities imposed by the subject through a failure to perceive correctly one of the attributes of the normal cards -- e.g., perceiving a red card as black.
Compromise Reactions
As we have already noted, a compromise perception is one in which the resultant perception embodies elements of both the expected attribute and the attribute provided by stimulation. Compromise reactions are, of course, limited to certain types of stimulus situations where a "perceptual middle ground" exists between the expectancy and the stimulus contradicting the expectancy. Our situation was one such. The subjects often perceived color in such a way as to make it more in keeping with, or to bring it nearer to, normal expectation about what colors go with what suits. Perhaps [p. 216] the best way to illustrate the point is to list the different colors reported when subjects were presented with red spade and club cards.
Brown Black on reddish card
Black and red mixed Olive drab
Black with red edges Grayish red
Black in red light Looks reddish, then blackens
Purple Blackish brown
Black but redness somewhere Blurred reddish
Rusty color Near black but not quite
Rusty black Black in yellow light
Lighter than black, blacker than red
Several questions arise at once. To what extent can the color compromise reactions be attributed to the action time required for the development of red? To what extent is compromise color due to the fact that our cards were not precisely "playing card" red in color? Answers to these questions can be provided in two ways.
First, the normal red cards (hearts and diamonds) were colored in precisely the same manner as the incongruous red cards (trick spades and clubs). This being the case, we would expect (if action time or off-color alone accounted for compromise) that there would be no difference between normal and trick red cards. There is, however, a striking difference. In reacting to trick red cards, 50 per cent of the subjects showed compromise responses; only 15 per cent showed such responses to the normal red cards. It should be noted, moreover, that if action time were a major factor, the normal cards, recognized on the whole at briefer durations, should have been more susceptible of compromise.
We have also checked on the frequency of compromise responses per card for those cards which elicited any compromise responses at all. When compromise responses do occur, will there be a difference in their frequency for normal and incongruous cards? Using percentages of exposures on which compromises occurred, weighted by total number of trial to recognition, we find that the percentage of compromises elicited by incongruous cards averages 63 per cent of the exposures preceding correct recognition. On the other hand, those normal cards which produced compromise responses did so on the average in only 32 per cent of the prerecognition exposures.
In sum, then, it seems highly unlikely that either "off-coloredness" or action-time alone accounted for these interesting responses. The question remains, of course, as to whether these two considera- [p. 217] tions facilitated the appearance of compromise. Although we lack publishable evidence on the point at this time, it seems to us on the basis of our own direct observations of briefly presented colors that both are important. Color, briefly presented, is subjectively more labile; one is somewhat less subjectively certain about its hue, and saturation is less. Given the decreased stability of the color in our briefly presented cards, it is not surprising that the normal expectation should readily lead to compromise. And when, moreover, the card falls somewhat short of "playing card redness," the tendency toward partial assimilation may become even greater.
Compromise reactions to black cards were considerably rarer than such reactions to the red cards. When they did occur, they were always given to trick black cards, never to normal ones. Only 11 per cent of the subjects showed such responses. Where they did appear, they constituted a weighted proportion of only 12 per cent of the prerecognition trials. The quality of the compromise responses to black trick cards was not strikingly different from that already reported for red cards.
Grayish tinged with red
Black with reddish gray background
Dark red
First black, then red, then black
Why so few compromise responses to the black cards? Several highly conjectural answers are worth examining. The first, and perhaps the most likely, has to do with the greater phenomenal stability of black at rapid exposure. There is, to be sure, a certain graying effect if the black is figural on white, which probably has to do with the poorly defined boundaries of such a figure at brief exposure. But the gray does not have the same quality of lability or instability of the chromatic card when presented for a brief duration (e.g., 10-50 ms.).
What, precisely, is involved in perceptual compromise? The most parsimonious assumption, we think, is that we are dealing with a special case of color assimilation, viz., assimilation to expectancy. The effect has been noted before, although it may not have been called "compromise." For example, Duncker (3) reports that a green felt leaf in hidden red illumination maintains its greenness better than an identically colored felt donkey in the same illumination. It [p. 218] is apparent from his subjects' color matches that neither stimulus object maintained green perfectly, but that the leaf did so more than the donkey. The color wheel used as the variable stimulus for matching contained green, orange, and white sectors. The green sector for the leaf was 60 degrees, for the donkey, 39 degrees. Like us, Duncker was dealing in his experiment with the problem of "expectancy color" -- i.e., that leaves are green -- and as in our case his subjects were compromising between an expected color (leaf green) and a given color (the resultant of leaf green in hidden red illumination). Very probably other experimenters, to name Grace Heider (5) and Fuchs as but two examples, obtained color compromises at least in part dependent upon their subjects' expectations about the color of the objects being partially obscured by a differently colored episcotister.
Disruption
Disruption is a gross failure of the subject to organize the perceptual field at a level of efficiency usually associated with a given viewing condition. Let us say that for normal cards the subject is able to perceive the color, suit, and number at from 20 to 50 milli-seconds. The same subject, faced with an incongruous card at 50 milliseconds may just begin reporting with some degree of confidence and only partial accuracy on the number and suit and color of the card before him. This may go on for several exposures as duration is increased, let us say, to 100 milliseconds -- well above his normal threshold range. At this point, the subject "loses confidence," becomes perceptually confused. Said our most extremely disrupted subject at 300 milliseconds in response to a red spade card:
I can't make the suit out, whatever it is. It didn't even look like a card that time. I don't know what color it is now or whether it's a spade or heart. I'm not even sure now what a spade looks like! My God!
Disruption was not frequent in terms of the number of exposures on which it appeared. But it did occur in 16 of our 28 subjects in response to trick cards. Among these 16 subjects and for those cards on which disruption occurred at all, it occurred on the average in 4 per cent of their prerecognition responses (percentages weighted by number of trials preceding recognition). Disruption typically occurred after the subject had "tried out" his available hypotheses [p. 219] and failed to come to a satisfactory recognition. In Woodworth's terms (8), the trial-and-check procedure had failed to yield a stable percept.
The kinds of disruption varied from subject to subject and even from card to card. In analyzing disorganized reactions, one can find any one or any combination of five disruptive effects. One might well expect that disruption would be selective, affecting those attributes of the stimulus with which the subject was having maximum difficulty.
Color disruption . . . . . . . . . . . . . . . . . . . . 4 S's
Form disruption . . . . . . . . . . . . . . . . . . . . 10 S's
Form-color disruption . . . . . . . . . . . . . . . . 3 S's
Number[1] disruption . . . . . . . . . . . . . . . . 2 S's
"Corner"[2] disruption . . . . . . . . . . . . . . . . 3 S's
Indeed, the figures above point to such selectivity -- form and color being the primary loci of incongruity. Having exhausted his resources in trying unsuccessfully to perceive the incongruous pairing of form and color, the subject might indeed be expected to end in the plight characterized by the typical remark:
"I'll be damned if I know now whether it's red or what!"
But what of number disruption? How to account for it? Only two subjects, to be sure, seemed to show disruptive uncertainty about the number of pips present -- in both cases after they had already perceived number correctly. In these instances one had the impression that the subjects had, so to speak, displaced their uncertainty upon an attribute of the stimulus which was not causing the real "perceptual trouble." Indeed, an additional exploratory experiment has indicated that in an extremely difficult incongruity situation such "displaced" disruptions are more common than in the present experiment. In that experiment a series of normal cards had interspersed at random among them two rather fantastic cards procured from a magic supply house: a card containing eleven diamonds but labeled in the corner with the notation for the fifteen of diamonds; the other was made up in the same way but was in the suit of spades and bore the notation of the fourteen of spades. In response to both cards subjects not infrequently ran the gamut of displacement: first [p. 220] being uncertain, properly, about the number, then suit, then color, then (though not frequently) about the size of the card.
Tempting though it might be to relate proneness to disruption to such concepts as Frenkel-Brunswik tolerance for ambiguity (4) or the concept of frustration tolerance (7), we do not at this time have any information which would warrant such an essay. One can, however, point to the phenomenon as a consequence of the "frustration" attendant upon failure to confirm a series of perceptual hypotheses. In this sense, the frustration is predominantly a perceptual matter (although some subjects grew irritated at their inability to "get" the stimulus).
A final word disposes of the frequency of disruption responses to the normal cards. There were none.
Recognition
In the perception of the incongruous stimuli, the recognition process is temporarily thwarted and exhibits characteristics which are generally not observable in the recognition of more conventional stimuli.
One specific way in which the recognition process is affected by the thwarting of well-established expectations is the emergence of a "sense of wrongness." The subject may either, even while "dominance" and "compromise" responses are continuing, suddenly or gradually begin to report that there is something wrong with the stimulus without being able to specify what it is that is wrong. It is not infrequent after such a report to witness the onset of perceptual disruption. But at the same time, such a "sense of wrongness" may also turn out to be a prelude to veridical recognition, for it often has the effect of making the subject change his hypotheses or give up his previous expectation about the nature of the stimulus.
Occasionally, as in 6 of our 28 subjects, the sense of wrongness may become focused upon a rather tangential, but, in point of fact, correct aspect of the incongruous stimuli and in so doing lead to a successful unmasking. These six subjects, prior to correct recognition, all reported that the position of the pips on the card was "wrong." All these responses were given either to spades printed in red or hearts printed in black at a time when the subject was calling the black hearts "spades" or the red spades "hearts."
[p. 221] What's the matter with the symbols now? They look reversed or something. (6SR)
The spades are turned the wrong way, I think. (4HB)
For those who do not have playing cards before them or who cannot remember the position of heart and spade pips, the former are printed with the point down in the top tier of pips and with the points up in the bottom, while spades are up-pointed in the top tier, down-pointed in the bottom.
Four of the six subjects who focused on this odd, and usually overlooked, positional arrangement of pips on a card finally achieved recognition. Two of the subjects failed to recognize their cards correctly in spite of unmasking this tell-tale feature.
Perhaps the greatest single barrier to the recognition of incongruous stimuli is the tendency for perceptual hypotheses to fixate after receiving a minimum of confirmation. As we have noted, some of our subjects persisted up to 1000 milliseconds in giving dominance responses to incongruous stimuli. Once there had occurred in these cases a partial confirmation of the hypothesis that the card in the tachistoscope was a black club or a black spade, it seemed that nothing could change the subject's report. One subject gave 24 successive black color-dominant responses to the black three of hearts, another 44 of them (both calling it the three of spades). Another persisted for 16 trials in calling it a red three of hearts. There were six instances in which subjects persisted in a color or form dominance response for over 50 exposures up to 1000 milliseconds, finally failing to recognize the card correctly.
Such fixation tendencies are, one might say, the chief block to perceptual learning. In another article on the effects of stress on perception (6), we pointed out that perceptual recklessness often resulted when a subject had to work under difficulties -- the formation and fixation of "premature" and incorrect perceptual hypotheses. It would appear, indeed, that working in incongruous situations where partial confirmation of expectancy can occur (the form of a spade is not so different from that of a heart, even if the colors are) has the same effect of inducing premature fixation.
As for correct recognition of incongruity following an unsuccessful period of trial-and-check, we have irreverently come to call
[p. 222] the response of some of our subjects the "My God!" reaction. For, to borrow a phrase from a distinguished literary critic, what occurs can well be characterized as "the shock of recognition."
One could, we suppose, liken the process of correct recognition to Köhler's description of insight. Indeed, it has some of the characteristics of sudden solution following unsuccessful attempts to master a situation. When a subject says: "Good Lord, what have I been saying? That's a red six of spades," there is no question about the sudden phenomenal emergence of the new perception.
Our reluctance in likening the phenomena to Köhler's description of insight is the suspicion that there is more to the matter than "sudden emergence." The uncertainty that sometimes comes before, the "sense of wrongness," the disruptions -- all these point to the gradual weakening of previous hypotheses before "sudden reorganization" can occur. Indeed, to match cases of "sudden phenomenal emergence," one sometimes finds a very gradual and almost timed approach to the correct recognition of incongruous object color. A subject viewing a red spade may start by reporting a red tint which gradually becomes redder on succeeding trials until he finally asserts that the card is a red spade.
Unfortunately, we have no light to throw on this particular variant of the "continuity-noncontinuity" sequence in perceptual reorganization.
Conclusions
Our major conclusion is simply a reaffirmation of the general statement that perceptual organization is powerfully determined by expectations built upon past commerce with the environment. When such expectations are violated by the environment, the perceiver's behavior can be described as resistance to the recognition of the unexpected or incongruous. The resistance manifests itself in subtle and complex but nevertheless distinguishable perceptual responses. Among the perceptual processes which implement this resistance are (1) the dominance of one principle of organization which prevents the appearance of incongruity and (2) a form of "partial assimilation to expectancy" which we have called compromise. When these responses fail and when correct recognition does not occur, what results may best be described as perceptual disruption. Correct [p. 223] recognition itself results when inappropriate expectancies are discarded after failure of confirmation.
Footnotes
[1] Number disruption is a loss of perceptual certainty about the number of symbols on the card.
[2] Corner disruption refers to confusion about what is in the corner of the card, e.g., reports that the pip in the corner is "wrong" or displaced or that the number in the corner seems out of place.
References
(1) BRUNER, J. S. Perceptual theory and the Rorschach test. J. Personal., 1948, 17, 157-168.
(2) BRUNSWIK, E. Wahrnehmung und Gegenstandswelt. Vienna: Deuticke, 1934.
(3) DUNCKER, K. The influence of past experience upon perceptual properties. Amer. J. Psychol., 1939, 52, 255-265.
(4) FRENKEL-BRUNSWICK, E. Intolerance of ambiguity as an emotional and perceptual personality variable. J. Personal., 1949, 18, 108-143.
(5) HEIDER, G. New studies in transparency, form and color. Psychol. Forsch., 1932, 17, 13-55.
(6) POSTMAN, L., AND BRUNER, J. S. Perception under stress. Psychol. Rev., 1948, 55, 314-323.
(7) ROSENZWEIG, S. Frustration theory. In J. McV. Hunt, Personality and the behavior disorders. New York: Ronald, 1944.
(8) WOODWORTH, R. S. Reenforcement [sic] of perception. Amer. J. Psychol., 1947, 60, 119-124.