Classics in the History
of Psychology
An internet resource developed by
Christopher D. Green
York University, Toronto, Ontario
ISSN 1492-3173
(Return to Classics
index)
DICTIONARY OF
PHILOSOPHY AND PSYCHOLOGY
JAMES MARK BALDWIN (1901)
Definitions Le - Loc
Leading of Proof: no concise foreign
equivalents. The operation bringing up to attention, among propositions admitted
to be true, certain relations between them which logically compel the acceptance
of a conclusion. (C.S.P.)
Leading Principle: Ger. leitendes
Prinzip; Fr. principe directeur; Ital. principio fondamentale.
It is of the essence of reasoning that the reasoner should proceed, and
should be conscious of proceeding, according to a general habit, or method,
which he holds would either (according to the kind of reasoning) always
lead to the truth, provided the premises were true; or, consistently adhered
to, would eventually approximate indefinitely to the truth; or would be
generally conducive to the ascertainment of truth, supposing there be any
ascertainable truth. The effect of this habit or method could be stated
in a proposition of which the antecedent should describe all possible premises
upon which it could operate, while the consequent should describe how the
conclusion to which it would lead would be determinately related to those
premises. Such a proposition is called the 'leading principle' of the reasoning.
Two different reasoners might infer the same conclusion from the same premises;
and yet their proceeding might be governed by habits which would be formulated
in different, or even conflicting, leading principles. Only that man's reasoning
would be good whose leading principle was true for all possible cases. It is
not essential that the reasoner should have a distinct apprehension of the leading
principle of the habit which governs his reasoning; it is sufficient that he
should be conscious of proceeding according to a general method, and that he
should hold that that method is generally apt to lead to the truth. He may even
conceive himself to be following one leading principle when, in reality, he
is following another, and may consequently blunder in his conclusion. From the
effective leading principle, together with the premises, the propriety of accepting
the conclusion in such sense as it is accepted follows necessarily in every
case. Suppose that the leading principle involves two propositions, L
and L', and suppose that there are three premises, P, P',
P''; and let C signify the acceptance of the conclusion, as it
is accepted, either as true, or as a legitimate approximation to the truth,
or as an assumption conducive to the ascertainment of the truth. Then, from
the five premises L, L', P, P', P'', the inference
to C would be necessary; but it would not be so from L, L',
P', P'' alone, for, if it were, P would not really act
as a premise at all. >From P' and P'' as the sole premises, C
would follow, if the leading principle consisted of L, L', and
P. Or from the four premises L', P, P', P'',
the same conclusion would follow if L alone were the leading principle.
What, then, could be the leading principle of the inference of C from
all five propositions L, L', P, P', P'',
taken as premises? It would be something already implied in those premises;
and it might be almost any general proposition so implied. Leading principles
are, therefore, of two classes; and any leading principle whose truth is implied
in the premises of every inference which it governs is called a 'logical' (or,
less appropriately, a formal) leading principle; while a leading principle
whose truth is not implied in the premises is called a 'factual' (or material)
leading principle. (C.S.P.)
Least Squares (method of): see ERRORS
of OBSERVATION.
Left-handedness: see DEXTRALITY.
Legal [Lat. legalis]: Ger. gesetzlich;
Fr. légal; Ital. legale. (1) Pertaining to law. (2)
Conformable to law. (3) Pertaining to law, as distinguished from equity.
(4) Defined or created by law, e.g. legal offences, legal disabilities.
Legal defence: one sufficient under the rules of law. Legal ethics:
the ethical rules governing the conduct of the legal profession. That may be
legal which is neither just nor honourable. 'Non omne quod licet honestum est,'
Dig., 1. 17, de diversis regulis iuris antiqui, 144. (S.E.B.)
Legal Fiction: Ger. Rechtsfiction;
Fr. fiction légale; Ital. finzione legale. The assumption,
as a fact, of what is not known to be such, made by authority of law to
promote justice.
It is generally done by the courts, sometimes by the legislature. Thus
the English courts of common law, in order to take jurisdiction of matters
of admiralty jurisdiction, anciently allowed a plaintiff to describe his
cause of action as arising at Havre, to wit, in Westminster, and refused
to allow the defendant to contest their right to entertain the case by
denying the averment as to Westminster. Cf. Maine's Ancient Law,
26.
Legal fictions furnish the means by which most nations develop their system
of procedure from formal into rational methods. See, as to their use in Roman
law, Sohm's Inst. of Roman Law, § 38; Hadley's Introd.
to Roman Law, 96. Wills causelessly disinheriting children could be set
aside, 'hoc colore, quasi non sanae mentis fuerint cum testamenta ordinarent.
Sed hoc dicitur non quasi vere furiosus sit, sed recte quidem fecerit testamentum,
non autem ex officio pietatis. Nam si vere furiosus sit, nullum testamentum
est' (Inst. of Just., ii. 18, de inofficioso testamento).
(S.E.B.)
Legend [Lat. legere, to read]: Ger.
Legende;
Fr.
légende; Ital. leggenda. An edifying tradition
which has grown up spontaneously and uncritically around some historical
personage, and which, though lacking in historic verity, is valuable in
the revelation it makes of the spirit and life of the people and time that
produced it.
In ecclesiastical history: legend is the story of a saint or other religious
personage which has grown up gradually in response to the requirements
of religious edification, and which, though containing a nucleus of truth,
is not historically reliable.
The legend differs from the myth in that it ordinarily develops about
a real personage, whereas the myth may be pure fiction, and ordinarily
arises out of a personification of some natural object or force. See MYTH.
Literature: EHRET, Allg. Gesch. d. Literatur d. Mittelalters im Abendlande
(1874-87); MILMAN, Hist. of Latin Christianity; LECKY, Hist. of Rationalism
in Europe. (A.T.O.)
Legislation [Lat. lex, law,
+ latio, a proposing]: Ger. Gesetzgebung; Fr. législation;
Ital. legislazione. (1) The act of making a law, by a legislator
or legislature. 'In legislation both contents of the rule are devised,
and legal force is given to it, by simultaneous acts of the sovereign power
which produce "written law." All the other law sources produce what is
called "unwritten law," to which the sovereign authority gives its whole
legal force, but not its contents, which are derived from popular tendency,
professional discussion, judicial ingenuity, or otherwise, as the case
may be' (Holland, Jurisprudence, chap. v. 66). (2) The law made
by a legislator or legislature.
Judicial legislation: the virtual making of law by judicial magistrates,
by declaring in their judgments that to be law which had not previously been
enacted or generally recognized as such. (S.E.B.)
Legitimate (in law) [Med. Lat. legitimatus]:
Ger. gesetzmässig,
legitim; Fr. légitime;
Ital. legittimo. Accordant with law; having the support of law;
legally entitled, especially of a child born in lawful wedlock (whether
begotten in wedlock or not).
Legitimate portion: that share of a parent's estate which, by the rules
of the civil law, cannot be willed away from the natural heir without some recognized
legal justification. (S.E.B.)
Legitimation [Fr.]: Ger. Legitimation;
Fr. légitimation; Ital. legittimazione. That by which
an illegitimate child is made legitimate in law.
By English and American common law there is no method of legitimation.
The later Roman law allowed it by virtue of a marriage of the parents at
any time after the conception or the birth of the child (Inst. of
Just., iii. 1, 2). Similar laws have been enacted in many of the United
States.
By English common law, legitimation has no extra-territorial force. Cf. Wharton,
Private Int. Law, chap. v. (S.E.B.)
Leibnitz (or Leibniz), Baron
Gottfried Wilhelm von.
(1646-1716.) Born at Leipzig, where his father
was professor of ethics, he was educated at Leipzig and Jena Universities.
He received a doctorate in law, but had become deeply read in scholasticism
and logic. For a period he had also studied Bacon, Hobbes, Kepler, Galilei,
Gassendi, and, to some extent, Descartes; and was for a time converted
to the mathematico-mechanical conception of nature. Under the patronage
of Baron Boineburg he prepared for a political life, became assistant to
Lasser in the preparation of a reformed code of Roman law, and member of
the Court of Appeals in Mainz (1670). He visited London, met Newton, Boyle,
and others, and became Fellow of the Royal Society. In Paris he was intimate
with Cassini and Huyghens. In 1676 he accepted a position in the court
of the Duke of Brunswick-Lüneburg, and (1678) was made counsellor
and member of the supreme court. Called to Berlin in 1698 by Princess Sophia
Charlotte, he established the Scientific Society, which has since become
Berlin University.
Lemma [Gr. lhmma,
gain, an assumption, premise]: Ger. Hülfssatz, Lehnsatz;
Fr. lemme; Ital. lemma. A theorem which interrupts the course
of development of a mathematical theory, but which is inserted to supply
a premise for one of the theorems.
This use of the word seems to go back to Euclid, at least; and even Aristotle
uses the word -- not a common one with him -- in connection with geometry, in
the first chapter of the Topics. With Aristotle, however, it means a
premise; and with the Stoics, more particularly, the major premise of a syllogism.
(C.S.P.)
Lese-majesty [Fr.], also written 'leze-majesty':
Ger. Majestätsbeleidigung,
Hochverrat; Fr. lèse-majesté;
Ital. lesa maestà. The crime of direct attack on the state,
or on its sovereign, his family, or his chief officers of government.
Formerly in Europe this crime was also regarded as comprehending offences committed
directly against God, such as sacrilege, blasphemy, or apostasy; being thus
termed lèse-majesté, divine (Merlin's Répertoire
de Jurisprudence, sub verbo). Of lèse-majesté humaine there
were several degrees, the offence being pushed so far in France as to include
embezzlement by public officials and unlawful assemblies. The crime of HIGH
TREASON (q.v.) was known by this name in England in the time of Glanvil (12th
century). The Roman law named this offence maiestatis crimen or more
fully 'crimen laesae, imminutae, diminutae, minutae, maiestatis,' Dig.,
x1viii. 4, ad Legem Iuliam Maiestatis; Smith's Dict. of Greek
and Roman Antiq. (maiestas); Heineccius, Antiq. Rom.
Syntagma, iv. § 46 f.) (S.E.B.)
Lessing, Gotthold Ephraim.
(1729-81.)
Educated at the Fürst nschule in Meissen, and at Leipzig, in philology
and theology. After 1748 he spent some time as journalist in Berlin. Went
to Wittenberg (1752) to complete his studies; returned to Berlin (1753)
to resume his work as journalist and critic. After two years spent in Leipzig,
he returned once more (1758) to Berlin. In 1760 he became secretary to
General von Tauenzien in Beslau, during the Seven Years' War; 1767, official
playwright and artistic director of the Hamburg theatre; 1770, librarian
of the ducal library at Wolfenbüttel.
Lewes, George Henry. (1817-78.)
An English Positivist, born in London. In youth a business clerk, he began
the study of medicine, but abandoned it for philosophy and psychology.
Spent two years in Germany, returning to London in 1840, and devoting himself
to literature. He was literary editor of The Leader (1849-54), and
founded the Fortnightly Review.
Liability (in law) [Fr. lier,
from Lat. legare, to bind]: Ger. Haftbarkeit; Fr. responsabilité;
Ital.
risponsabilità. Such a relation by one to another as
will or may support an action by the latter against the former.
The maker of a note, as soon as it is delivered, comes under a liability
to the holder, which may support an action, and will, if the note be dishonoured
when due. The contingent liability of the endorser of a note becomes
an absolute liability when the note is dishonoured, and due demand
and notice follow. Liability is viewed by Austin 'as a sanction' imposed
by law as a penalty for disobedience of law. But an unintentional act of
violence to another may impose an actionable liability, though there was
no intent to disobey the law. Liability for an act whereby another is injured
can be rested better on the natural obligation to act in contemplation
of the natural tendency, under existing circumstances known or knowable,
of the act to do harm (see Holmes on the Common Law, 79, 81, 162).
Limited liability: (1) a liability of shareholders in a business corporation
or joint-stock company, limited by law to the amount of their subscriptions
for shares; (2) the restricted liability of shipowners for accidents occurring
without their fault (see U.S. Revised Statutes, §
832). Individual liability: that which one holding a representative position
as executor, cashier, or governor, may incur by contracting on his personal
credit, though not for his personal benefit. The common-law maxim is Ubi
ius, ibi remedium. (S.E.B.)
Libelt, Karol. (1807-75.) Educated
at Berlin, under Hegel, in philosophy. Wrote the gold medal essay on Spinoza
(1828); received his doctorate in philosophy (1830). Took part in the Polish
revolution in that year, and was imprisoned nine months. In 1840 he opened
a private school at Posen, and edited two journals. His life was given
to literature. He was again imprisoned (1846-8), and his journal suppressed
(1849). Took a prominent part in the reorganization of Great Poland, and
protested in the Parliament at Frankfort against the incorporation of Great
Poland in Germany. He was the first famous Polish philosopher.
Liberalism [Lat. liber, free]:
Ger. Liberalismus; Fr. libéralisme; Ital. liberalismo.
(1) The personal disposition to free and untrammelled thought and action.
(2) The social sentiment which welcomes reforming and progressive opinion
and action.
Liberalism is opposed to conservatism in both these meanings; but a
certain relative balance between them is necessary to stable social organization,
in which the writer (Social and Eth. Interpret., chap. v.
§ 3; cf. Royce, Psychol. Rev., v. 1898, 113) has likened
them to habit and accommodation in the individual's life. Extreme liberalism,
taking the form of a disposition to accept innovations as such, is called
radicalism.
Literature: see SOCIOLOGY, and SOCIAL PSYCHOLOGY. (J.M.B.,
F.H.G.)
Liberty (1) and (2)
Libertarianism [Lat. libertas]: Ger. Freiheit; Fr. liberté;
Ital. libertà. (1) See FREEDOM (various meanings), and WILL; (2)
Ethical INDETERMINISM (q.v.), also the references made under (1). (J.M.B.)
Liberty (political): see FREEDOM
(political and social).
Liberty (religious): Ger. Religionsfreiheit;
Fr. liberté religieuse; Ital. libertà religiosa.
The legally secured right of the individual to hold and practise without
interference any form of religious belief and worship he may choose, in
so far as the exercise of his prerogative does not conflict with the fundamental
political and social principles of the society to which he belongs.
The history of religious liberty in modern times begins with the edict
of toleration by Constantine in 313 A.D. Throughout the middle ages the
enforcement of conformity to prescribed form of belief was regarded as
a duty. The Reformation did not effect much advance in freedom, but Catholic
and Protestant alike claimed the right of coercion. A considerable advance
was made at the Peace of Westphalia in 1648, when equal rights were accorded
to professors of the Catholic, Lutheran, and Calvinistic faiths. The French
Revolution marked the beginning of a new era, in which the principle of
religious freedom in its widest sense has gradually secured almost universal
recognition.
Literature: GIBBON, Decline and Fall of the Roman Empire; GUIZOT, Hist.
of Civilization in Europe; VOLTAIRE, Essay on Toleration; LOCKE, Essays; LECKY,
Hist. of Rationalism; BANCROFT, Hist. of the United States. Cf. ERASTIANISM,
and GALLICANISM. (R.M.W.)
Lie [AS. leogan]: Ger. Lüge;
Fr. mensonge; Ital. menzogna. Any intentional deception of
another by positive misrepresentation. Cf. EQUIVOCATION.
The essence of the lie rests in the intention to deceive; yet the means
of the deception, by positive misrepresentation -- as contrasted with either
negative suggestion (suggestio falsi) or omission of truth (suppresio
veri) -- seems, though casuistical, to be well established. The following
example from Macaulay (Hist. of England, chap. ix) illustrates
this 'distinction without a difference.' Bishop Compton, who had invited
William of Orange to invade England in 1688, is asked by King James if
there is any truth in the statement in William's manifesto that some spiritual
peers had invited him; he replies: Sir, I am quite confident that there
is no one of my brethren who is not as guiltless as myself in this matter.'
Macaulay remarks: 'The equivocation was ingenious; but whether the difference
between
the sin of such an equivocation and the sin of a lie be worth
any expense of ingenuity may perhaps be doubted.'
The question of the ethical justification of a lie is also quite apart; whether
right or not, a lie is a lie 'for a' that.' See VERACITY, and cf. CASUISTRY.
(J.M.B.- H.S.)
Life and Organic [AS. hlifian.
Gr. o ganon]: Ger. Leben, Lebewesen
(living
being), organisch; Fr. vie, organique; Ital.
vita,
organico.
A form of organization found in certain material things, having the properties
of self-perpetuation, for a longer or shorter time, and of reproduction
in some form, and further distinguished by certain characters described
as vital properties or properties of LIVING MATTER (q.v.). Matter having
this organization and these characters is called 'living' or 'organic,'
as opposed to 'dead' or 'inorganic' matter. Cf. also PROTOPLASM.
The theories of life have always turned on the form of organization
displayed, as contrasted with other forms, such as notably the chemical.
The problem seems little nearer solution now than in the time of the speculations
of Aristotle. To Aristotle the soul was the 'form' or 'formal cause' of
the organized body, the matter of which was the 'material cause' of the
living creature. The scholastic theory of 'vitality' or 'vital force' postulated
a principle additional to those of mechanical action and chemical organization,
a view which laboured under the obscurity of the word 'force,' and came
to be directly challenged when the generalization of the CONSERVATION OF
ENERGY (q.v.) was announced. This difficulty, i.e. of determining whether
vital phenomena are subject to the law of conservation, has never been
overcome. The question is as to whether or not vital changes, such as those
of development and growth, can be adequately accounted for as transformations
of the known forms of energy; and if not, what more is necessary. Current
views divide into (1) the mechanical or chemical, which holds that vital
phenomena are entirely explainable in terms of mechanical and chemical
change; (2) vitalism or neo-vitalism, holding to a 'something over,' which
takes the form (a) of a new force or energy (e.g. growth-force or
bathmism of Cope; 'genetic energy' of Williams), (b) a property
of 'self-adaptation' (Henslow) or 'direction' (Eimer), or (c) the
assumption of a form of 'so-called' directive force which, while diverting,
guiding, or shunting physical energy, yet does not alter its amount. This
last view often makes consciousness the new agent, and represents a distinct
tendency in discussion to restate the question in terms of a dualism between
matter and mind rather than between matter and life; the additional point
being assumed, or directly advocated, that life and mind are coterminous.
This does not alter the essential conditions of the problem, although it
is held to strengthen the position of vitalism by making accessible to
it the facts and arguments in support of some sort of causal activity of
mind. Philosophically, however, it has the distinct advantage of reducing
two dualisms to one, and of bringing the question within the lines of one
of the broadest and most critical problems, i.e. that stated by Aristotle
in terms of 'matter and form,' discussed by religious philosophers under
the heading of teleology, and taking the form in modern metaphysics of
the inquiry as to the final category of organization (matter and motion,
dualism of body and mind, or monism in some higher term). Cf. MIND AND
BODY, ORGANIZATION, TELEOLOGY, and the remarks on teleology under HEREDITY.
The discussion labours under the confusion hidden in the words CAUSE, FORCE,
ENERGY (which should also be consulted). Cf. also ORIGIN OF LIFE.
As to the explanation of the facts involved, the rival theory to vitalism
is natural selection, which is at its best in explaining the apparently
vital directive movement in evolution, but weaker in explaining individual
growth and development. On the other hand, vitalism makes its strongest
stand in what is called the developmental mechanics of the individual,
where the facts of REGENERATION (q.v.) and organic accommodation, it is
held, can only be described in vitalistic terms and illustrate the inscrutable
mystery of life (cf. Wilson, The Cell, 329). It is interesting to
note, as illustrating the truth of this opposition, that the new vitalism
is current for the most part in countries -- notably Germany and the United
States -- where the problems of ontogeny are especially investigated, while
in other countries -- notably England -- vitalism in any form is criticized
as mysticism.
Literature: ARISTOTLE, zoological writings; WUNDT, Logik, II. i. 3,
4, 'd. Logik d. Biol.'; COPE, Primary Factors of Organic Evolution; VERWORN,
Gen. Physiol. (Eng. trans.); WILLIAMS, The Genetic Energy of Organisms, Science,
May 27, 1898; SANDEMAN, The Problems of Biol.; EIMER, Organic Evolution (Eng.
trans.); WILSON, The Cell; OSBORN, From the Greeks to Darwin; BROOKS, Foundations
of Zool., v. BUNGE, Lehrb. d. Physiol. (1889); DU BOIS-REYMOND, Ueber d. Grenzen
d. Naturerkenntniss; JAPP, Pres. Add. Chem. Sec. Brit. Assoc., Report, 1898;
LLOYD-MORGAN, Monist, Jan., 1899; WARD, Naturalism and Agnosticism; and most
of the general works on the BIOLOGICAL SCIENCES (q.v.). (J.M.B.,
C.L.L.M.)
Life (spiritual) [ME. lif]:
Ger. geistiges Leben; Fr. la vie spirituelle; Ital. vita
spirituale. (1) That activity of a self-conscious being which gives
rise to moral, aesthetic, and religious experiences.
(2) In theology: the divine life which is manifested in Christ, and
in which the believer is by faith enabled to participate.
The spiritual life represents the central mystery of the Christian faith. The
new birth involves the throwing away of the old carnal life and the putting
on of a new life, of which the central principle is to be the spiritual energy
of Jesus Christ. In the New Testament the spiritual life is not only represented
as ideally rich and complete, but also as in its nature eternal as the life
of God. (A.T.O.)
Light: see VISION.
Light of Nature [trans. of Lat.
lumen
naturae or naturale, a term used by Aquinas, Summa Theologiae,
Pt. I, qu. 12, art. 13, and elsewhere. It is not necessary to suppose that
he borrowed the term from the passage of Aristotle's De Anima, 430
a, 14, where the creative intellect is compared with light]: Ger. natürliches
Licht; Fr. lumière naturelle (Pascal); Ital. lume
naturale (Galileo). A natural power, or instinct, by which men are
led to the truth about matters which concern them, in anticipation of experience
or revelation. See LUMEN (also for literature).
The phrase is used in contradistinction to supernatural light. Tucker's Light
of Nature pursued is a book written as a mild reaction against Locke and
the Associationalists in the direction of the philosophy of common sense. (C.S.P.)
Light Sensation: Ger. Lichtempfindung;
Fr. sensation lumineuse; Ital. sensazione luminosa. Visual sensation.
See VISION. See also BRIGHTNESS. (E.B.T.)
Likeness or Resemblance
(consciousness of) [AS. lic, in gelic, like]: Ger. Aehnlichkeit;
Fr. ressemblance; Ital. somiglianza, or rassomiglianza.
Two mental objects or contents are said to be alike for consciousness when
in respect to certain features one might be taken for the other. This is
hit off in the current conundrum: 'What is most like a rain-drop?' Answer:
'Another rain-drop.' Such objects are said to have likeness, to be alike,
or to resemble each other.
Theories of likeness are based on partial identity of the two mental
contents (cf. RESEMBLANCE); partial recognition of one in the other; partial
assimilation of one to the other, or of both to a third; or on an active
adjustment to one which holds also in part for the two. The last of these
views, to which the writers adhere, is well summed up by Ward: 'Presented
objects become related as "like" either in virtue of the active adjustment
to a change of impression which their partial assimilation defeats, or
in virtue of an anticipated continuance of the impression which this assimilation
confirms' (art. Psychology, in Encyc. Brit., 9th ed., xx.
180). Cf. the classification given under RESEMBLANCE, and the topics there
referred to.
The case in which two things are alike in all respects -- are taken one for
the other -- is mentioned under INDISCERNIBLES, and DIFFERENCE. (J.M.B.-
G.F.S.)
Limen [Lat.]: equivalent to THRESHOLD (q.v.),
which is already current, and is preferred.
The adjectives 'liminal' (at the threshold), 'subliminal' (below the threshold),
and 'supraliminal' (above the threshold) are useful. Cf. LIMITS OF STIMULATION.
(J.M.B.)
Limitative [Lat. limitare, to
enclose]: Ger. limitativ (Urtheil); Fr. limitatif;
Ital. limitativo. (1) Applied to a third quality of judgments, additional
to affirmative and negative. The idea of such a third quality originated
among the Romans from the difference between 'homo non est bonus' and 'homo
est non bonus,' the latter being the limitative.
(2) Setting limits in the sense (2) given under LIMITING NOTION (q.v.).
It is one of the numerous cases in which accidents of language have affected
accepted logical forms without any good reason. Boethius and others applied
the infinitation to the subject also, which De Morgan has shown makes a valuable
addition to logic. Wolff, however, limited the modification to the predicate,
without showing any serious reason for such application. Kant adopted it because
it rounded out his triad of categories of quality. His defence, as reported
by Jäsche, is that the negative excludes the subject from the sphere of
the predicate, while the unendliche, limitative, or infinite judgment puts it
into the infinite sphere outside the predicate. It is to be remarked that Kant
regards a positive mark as differing per se from a negative one, and,
in particular, as having a far narrower extension. Like most of the old logicians,
he virtually limited the universe of marks to such as arrest our attention.
If that had been explicitly and consistently done, it would have constituted
an interesting particular logic, in which there would be a material and not
merely formal difference between affirmative and negative facts. It is probable
that Kant also understood the affirmative proposition to assert the existence
of its subject, while the negative did not do so; so that 'Some phoenixes do
not rise from their ashes' would be true, and 'All phoenixes do rise from their
ashes' would be false. The limitative judgment would agree with the affirmative
in this respect. This was probably his meaning, and he did not observe that
his limitative judgment, 'The human soul is immortal (nichtsterblich),' may
be construed as equivalent to the conjunctive judgment, 'The human soul is not
mortal, and it is the human soul.' No doubt Kant would have seen a world of
difference between these two assertions. In that case he should have adopted
a fourth quality, 'The human soul is not immortal.' (C.S.P.)
Limiting Notion: Ger. Grenzbegriff;
Fr. notion-limite; Ital. concetto limite. (1) A term used by Kant
in a single passage of the Krit. d. reinen Vernunft (1st
ed., 255) to signify that a NOUMENON (q.v., ad fin.), which is a thing
in itself regarded as an object of reason, is something to which experience
cannot attain, but is the inconceivable something behind the phenomena. The
passage reads: 'Der Begriff eines Noumenon ist also bloss ein Grenzbegriff,
um die Anmassung der Sinnlichkeit einzuschränken, und also nur von negativem
Gebrauche.' (J.M.B.- C.S.P.)
(2) The notion of what would be the limiting or extreme case of the
application of a truth or principle.
The limiting notion in this sense involves abstraction from the conditions
of particular existence; and it also fulfils an ideal. Hence it is both limitative
and negative with reference to existence in the sphere of the particular. Cf.
LIMITATIVE (2), and LIMITS (in mathematics). The validity of Kant's negative
conclusions regarding God, freedom, and immortality turns upon the construction
of the negative character attributed to the limiting notion, i.e. upon the theory
of reality of the noumenal or universal sort. (J.M.B.)
Limits (in mathematics)
[Lat. limes, a boundary]: Ger.
Grenze; Fr. limite;
Ital. limite. A fixed quantity towards which we conceive or prove
a variable quantity to approach, so that their difference becomes infinitesimal,
though it never entirely disappears, is called a limit.
A simple example is that of the series 1/2 + 1/4 + 1/8 + 1/16 + &c., in
which each term is half the preceding one. It is evident that the sum of the
terms will always be less than 1 by the last term, thus 1/2 + 1/4 + 1/8 = 1
- 1/8, &c. Now since, by halving a quantity continually, we can make it
less than any assignable quantity, it is clear that there is no limit to the
possible smallness of the difference between the sum and 1. On the other hand,
the sum can never become equal to 1, because we shall always have a difference
equal to the last term of the series. In this case the value 1 is said to be
the limit of the sum of the series. (S.N.)
Limits (of
Stimulation (1) and (2) of Sensation): Ger. Grenzwerthe; Fr.
étendue; Ital. limine. (1) The limits beyond which, in
either direction, stimulation of a sense-organ is ineffective; (2) the boundaries
of a sensation series or continuum. (E.B.T.)
In intensity: the extremes of intensity of stimulus that give sensations.
The lower limit of sensation, the minimal sensation, the limen or THRESHOLD
(q.v.), is the just noticeable intensity of sensation. The upper limit
of sensation, or the maximal sensation, is that due to the most intense
stimulus. The RANGE (q.v.) of sensation, according to Wundt, is measured
by the maximal sensation divided by the threshold.
Wundt introduced the term Reizhöhe for the upper limit. The existence
of the lower limit is in part due to the interference of physical and physiological
stimuli, in part to physiological inertia and dispersion, and in part may perhaps
be regarded as a case of subconscious stimulation. The upper limit is perhaps
due to the injury of the sense-organ by intense stimulation. Cf. FECHNER'S LAW,
WEBER'S LAW, and PSYCHOPHYSICAL METHODS. (J.McK.C.)
In quality, &c.: the term 'limits of stimulation,' with its correlate
'range of stimulation,' applies also to sensation qualities. We may determine
qualitative limits in two different ways. The upper and lower limit of
tone stimulation, e.g., may be given as the greatest and least number of
vibrations in the second that produce a tone sensation (see Auditory Sensation
under HEARING). Or we may inquire as to the least number of vibrations
necessary for the cognition of a tone of given vibration rate: this number
seems to vary between 2 and 20. Moreover, every sense-organ shows limits
with respect to the time intervals of stimulation, while the eye and skin
have also limits with respect to extent.
Literature: KÜLPE, Outlines of Psychol., 34; WUNDT, Physiol. Psychol.
(4th ed.), i. 334 f. (E.B.T.)
Lindner, Otto. (1820-67.) Born and
educated at Breslau, he devoted himself especially to philology and philosophy.
He became a private instructor in Berlin, and in 1847 took a position on
the Vossische Zeitung, becoming editor-in-chief in 1863.
Line of Beauty: Ger. Schönheitslinie;
Fr. ligne de beauté; Ital. linea di bellezza. A term
applied by Hogarth (1745) to a serpentine line, which he regarded as the
most beautiful outline.
In his Analysis of Beauty (1753) Hogarth styled the serpentine line
'line of grace' (see GRACE), and restricted the term 'line of beauty' to the
waving line (~). He regarded 'variety' as the ground of its aesthetic
value. (J.H.T.)
Line of Direction: Ger. Richtungslinie
(-strahl); Fr. ligne de direction; Ital. linea di direzione.
The line of direction is the straight line connecting a luminous point
with the nodal point of the 'reduced' eye, and prolonged to meet the retina.
It gives the position on the retina of the luminous point. See Fig. 7 under
VISION.
Literature: HELMHOLTZ, Physiol. Optik (2nd ed.), 91, 742; WUNDT, Physiol.
Psychol. (4th ed.), ii. 98; SANFORD, Course in Exper. Psychol., expts. 106,
117; AUBERT, Physiol. Optik, 600; FICK, in Hermann's Handb. d. Physiol., III.
i. 64; HERING, ibid., 349; Beitr. z. Physiol., i. (1861) 25 ff. Cf. LINE OF
VISION. (E.B.T.)
Line of Regard: Ger. Blicklinie;
Fr. ligne de regard
(Helmholtz,
Physiol.
Optik, Fr.
trans., 599); Ital. linea di mira. The straight line connecting
the point of regard or fixation point with the centre of rotation of the
eye. See Fig. 7 under VISION.
Literature: HELMHOLTZ, Physiol. Optik (2nd ed.), 91, 617, 679; SANFORD,
Course in Exper. Psychol., 119, and expts. 176, 177, 219; WUNDT, Physiol. Psychol.
(4th ed.), ii. 99, 121; AUBERT, Physiol. Optik, 419, 646; HERING, in Hermann's
Handb. d. Physiol., III. i. 441. See LINE OF VISION. (E.B.T.)
Line of Vision or
Line
of Sight: Ger. Gesichtslinie; Fr. rayon visuel; Ital.
linea
visuale. A straight line joining the fovea with the fixation point,
and making with the OPTICAL AXIS (q.v.) an angle of about five degrees.
The line may also be defined in terms of the nodal point of the 'reduced'
eye, and accordingly termed the 'principal ray of direction.' It is practically
coincident with the LINE OF REGARD (q.v.; see also Fig. 7 under VISION).
Literature: WALLER, Human Physiol., 412; Helmholtz, Physiol. Optik (2nd
ed.), 91, 617; WUNDT, Physiol. Psychol. (4th ed.), ii. 99, 121; AUBERT, Physiol.
Optik, 415, 417; FICK, in Hermann's Handb. d. Physiol., III. i. 59; HERING,
ibid., 349. (E.B.T.)
Linguistic Science: see PHILOLOGY,
LANGUAGE, and PHONETICS.
Listing's Law: Ger. Listing'sches
Gesetz der Augenbewegungen; Fr. loi de Listing pour les mouvements
de l'oeil; Ital. legge di Listing.
If the LINE OF REGARD (q.v.) is carried from the primary to any other
position, the torsion of the eyeball in this new position is as it would
be if the eye had turned about a fixed axis, standing at right angles to
both directions of the line of regard' (Helmholtz).
The law has two corollaries: (1) that in movements from the primary
position there will not be, and (2) that in movements from secondary position
to secondary position there will be, rotation about the line of regard.
Cf. Sanford, Course in Exper. Psychol., expt. 131 b, and
App. I.
Literature: HELMHOLTZ, Physiol. Optik (2nd ed.), 623; WUNDT, Physiol.
Psychol. (4th ed.), ii. 116; SANFORD, Course in Exper. Psychol., expt. 131 b;
AUBERT, Physiol. Optik, 646, 653; LE CONTE, Sight, 147; HERING, Binocul. Sehen
(1868), 64, 68; RUETE, Lehrb. d. Ophthal., i. 37. (E.B.T.)
Littré, Maximilien
Paul Emile. (1801-81.) Born and educated for medicine in Paris. In
1830 he fought on the barricades in Paris as a republican. Shortly after
this he began writing scientific articles for
Le National. In 1839
he became a member of the Académie des Inscriptions et Belles-Lettres.
In 1840 he read the works of Auguste Comte and became a leader among the
advocates of the Positive philosophy. He took up the
Histoire littéraire
de la France upon the death of Fauriel in 1844. In 1863 he presented
the Academy with the first part of his Dictionnaire de la Langue Française;
he continued also his contributions to medical literature. Member of the
Assembly in 1871, and life senator after 1875. Member of the Académie
Française after 1874.
Living Matter: Ger. lebendiger Stoff;
Fr. substance vivante; Ital. sostanza (or materia) vivente.
Matter in the peculiar unstable or labile condition which enables it to manifest
the properties or functions of life. These properties are (1) nutrition in its
widest sense, as including all the processes of anabolism and katabolism. (2)
Reproduction: the power of changing dead (food) matter into itself, thus reproducing
itself and increasing in amount up to the limit of the food supply. All known
living matter has thus arisen from previous living matter. (3) Irritability,
including the fundamental functions of conductivity and contractility: the property
of living matter by which it is enabled to respond to stimuli, i.e. to maintain
continuously internal adjustments to external changes, an essential characteristic
of life. (C.F.H.)
Chemical Composition. Protoplasm is not a unitary chemical substance,
but it is a complex mixture in ever-varying proportions of very many different
substances. The quest for a definite chemical formula for protoplasm has
proved vain. Living substance can at present be defined, not in terms of
chemical composition, but in terms of its morphological and physiological
properties. The nature of the bond which holds these diverse substances
together and maintains the integrity and continuity of the life process
during the continual flux of the elements of its physical basis, which,
in short, renders living substance self-perpetuating -- this is the problem
of life, and it is apparently as far from solution to-day as it was in
the time of our fathers, who cloaked their ignorance under the term 'vitalism.'
Cf. LIFE.
Vital manifestations, however, so far as they have yet been analysed,
reduce themselves to physico-chemical forces, from which it may be inferred
that the distinguishing features of living things depend upon the nature
of the interrelation of these forces rather than upon any special super-physical
force. But it does not at all follow that the synthesis of living substance
would be possible, even if we were able to make artificially all the proximate
chemical compounds which are mingled in its structure. For, as Oscar Hertwig
has pointed out, none of the protoplasm now living has been formed in any
other way than by the propagation of pre-existing protoplasm; it is, therefore,
the product of an exceedingly long historical development.
At present, however, our knowledge of the molecular structure of the
proximate ingredients of protoplasm is very meagre. The simplest of these
organic compounds have very large molecules, often with more than a thousand
atoms. The formula for a molecule of albumen has been given as C72
H106 N18 SO22, and for haemoglobin, C600
H960 N154 Fe1 S3 O179.
This peculiarity alone is sufficient to explain many of the properties
of organic substances, such as their inability in most cases to dialyze
and to diffuse rapidly in solutions. For some interesting speculations
growing out of the properties of the twelve elements chiefly represented
in organized bodies (viz. C, N, S, H, O, P, Cl, K, Na, Mg, Ca, Fe), see
Spencer's Principles of Biology and Verworn's General Physiology.
The latter author gives a brief account of Pflüger's interesting researches
on the rôle of cyanogen, CN, in the metabolism of proteids, from
which the conclusion is drawn that the essential difference between living
and dead proteid is the presence of the radical cyanogen in the former,
but not in the latter. Further study of the properties of some of the non-living
compounds of this radical brings out some curious resemblances with living
proteid (notably in their tendency towards transformation and polymerization),
and Pflüger concludes: 'Accordingly, I should say that the first proteid
to arise was living matter, endowed in all its radicals with the property
of vigorously attracting similar constituents, adding them chemically to
its molecule, and thus growing ad infinitum. According to this idea,
living proteid does not need to have a constant molecular weight; it is
a huge molecule, and undergoing constant, never-ending formation and constant
decomposition, and probably behaves towards the usual chemical molecules
as the sun behaves towards small meteors.'
Another, and perhaps the simplest, method of considering the problem
of living matter, though it suffers, as do all others, from the impossibility
of concrete demonstration, concerns itself not with the analysis of the
material elements of living substance into units whose quantitative formulas
somehow are supposed to represent the potency of the substance, but with
a synthesis of the several energies after the analogy of the composition
of forces in mechanics. This theory does not suppose that the several grades
of vitalized matter differ in ways that can be expressed by chemical formulas,
but the forces merged into the living entity are conceived of as constituting
a unitary force compounded from the more elementary ones, merged in it
in such a way that, if our knowledge were complete enough, the several
vital activities might be expressed somewhat as are the complex curves
of geometry. The essential point of this theory lies in its insistence
that the vital activity is a unit and not a compound thing. A method of
dynamic notation is greatly needed in this connection.
Microscopic Structure. Casual examination of protoplasm, even
with rather low magnifying powers, shows that it is by no means homogeneous;
and the more thorough the examination, the more forcibly is this differentiation
impressed upon the observer. When properly prepared by suitable reagents
it is seen to be composed of a more fluid portion or plasma (cytolymph,
enchylema, or ground-substance), and a more dense material, the spongioplasm.
The latter must not, however, be regarded as normally a solid, for living
substance as a whole is unquestionably liquid.
The theories of protoplasmic structure fall into two general classes:
those which regard the more fluid plasma as the essential vital part, and
those which regard the more dense framework as the essential, the interstitial
substance serving simply as a vehicle for nutrition, &c. Though the
former of these views is supported by several eminent authorities, yet
the great majority of observers hold to the latter conception in some form,
or regard both ingredients as equally essential. But these observers are
by no means agreed as to the nature of the spongioplasm. We have, accordingly,
from this point of view, four theories of protoplasmic structure: --
I. The granular theory. The miscroscope does unquestionably reveal the
presence of numerous granules both in living and in prepared protoplasm,
and they have given rise to much speculation. They have been variously
termed micellae, pangens, ideoblasts, ideosomes, plastidules, bioplasts,
gemmae, biogens, biosomes, microsomes, &c. The latter term is perhaps
the most unobjectionable, as involving less of hypothetical interpretation.
Many authors regard these bodies as a sort of biological unit of lower
order than the cell. The existence of such units was postulated from theoretical
grounds by several of the earlier authors (Spencer's 'physiological units,'
Nägeli's micellae,' Darwin's 'gemmules,' &c.), and they figure
very largely in the writings of several recent authors (notably Weismann
and Altmann).
II. The filar theory. According to this conception, usually ascribed
to Flemming, the spongioplasm is composed of interlacing threads which
do not unite to form a reticulum.
III. The reticular theory. The structure is conceived of as a mass of
threads which are combined into a more or less regular network. This reticular
appearance is very often observed, though it is not always possible to
prove that the fibres actually anastomose. The microsomes are often seen
in connection with it, either at the nodes of the reticulum or strung along
the fibres. Probably the majority of competent observers, at least until
very recently, have held to this view.
IV. The alveolar theory. This we owe primarily to Bütschli, whose
researches upon artificial foams lend some support to the belief that protoplasm
is a microscopic foam or emulsion of two liquids of different densities.
The fibres of the other theories are the walls of the vesicles of this
emulsion as seen in optical section. This idea is being adopted, wholly
or partially, by a rapidly increasing number of both zoologists and botanists,
particularly those of the younger generation.
Probably no one of these conceptions expresses the whole truth. Indeed,
Wilson has very recently brought forth strong direct evidence that the
alveolar spheres, microsomes, and some, at least, of the true thread structures
of the cytoplasm, are all different gradations of one structure. He agrees
with Kölliker that 'no universal or even general formula for protoplasmic
structure can be given,' and adds; 'Life in its full sense is the property
of the cell-system as a whole rather than of any one of its separate elements.
Nevertheless, we are perhaps justified in maintaining that the continuous
substance is the most constant and active element, and that which forms
the fundamental basis of the system, transforming itself into granules,
drops, fibrillae, or networks in accordance with varying physiological
needs.'
Properties. Since the dawn of science, there has been a strong
tendency towards mysticism in the treatment of all phenomena connected
with life. Of the commonly enumerated fundamental physiological properties
(spontaneity, irritability, contractility, growth, reproduction, &c.),
all, except possibly the last, when rigidly defined, can be shown to be
manifested in some degree under proper conditions by dead substances. The
specific living substance contains no elements not found in unorganized
matter, though, as we have seen, these elements are probably arranged in
a characteristic manner. If we follow Verworn and say that 'the life-process
consists in the metabolism of proteids,' it is plain that there is no room
here for any metaphysical agency, since metabolism is merely the sum of
the chemical processes going on within the body.
The present tendency is to study the properties of living beings in
the same way as we do the properties of other physical bodies, viz. experimentally.
This, of course, has always been the method of physiology, but of late
it has been widely extended into the fields of experimental morphology
and experimental embryology, in the hope of determining, not only what
the phenomena of these sciences are, but how they came to be so. Since
all vital manifestations can probably be reduced to responses of the living
material to the forces impinging upon it from the environment, this study
resolves itself into two problems, viz. the intrinsic properties of the
reacting substance as such, and the specific effects of outer forces upon
this substance.
The former problem includes the study of the protoplasmic constants,
such as general chemical properties, physical structure, heredity, &c.,
and is far less advanced than the latter. Since in nature these two factors
are always represented in every vital phenomenon, for scientific purposes
they must be artificially separated, either by logical analysis or actually,
under experimental conditions. Hence the motive for the present tendency
towards experimental biology. It must be admitted that this analysis has
not yet been carried very far. Even HEREDITY (q.v.), the name given to
the self-perpetuation of vital processes from generation to generation,
is not rigidly true to type, i.e. variations occur, whose connection with
external conditions cannot always be traced, and the embryologists are
divided into opposing schools on the question of the relative importance
to the course of the ontogeny of intrinsic, i.e. inherited, factors and
those which are extrinsic, i.e. determined by the direct action of the
environment. This is the modern phase of the old controversy between PREFORMATION
and EPIGENESIS (see those terms, and cf. Wilson, The Cell in Development
and Inheritance, particularly the last chapter).
All the phenomena of growth, however much they may be dependent upon
inherent structure, are also affected variously by environmental influences.
For instance, the necessity for the division of a growing body into units
(cells) of small size is due simply to the fact that during growth the
absorbing surface, by which alone nutriment can enter the protoplasm, increases
as the square of the radius, while the protoplasmic mass, in which the
consumption of nutriment takes place, increases as the cube of the radius.
Obviously a limit is soon reached beyond which nutriment cannot be absorbed
as fast as it is consumed, and either growth must cease or the mass must
be divided so as to permit an increase of surface without a corresponding
increase of mass. One of the most striking cases of the influence of external
forces upon the course of development has been recently brought out by
Loeb, who finds that unfertilized eggs of sea-urchins, if put into water
containing a definite proportion of magnesium chloride for a short time
and then transferred to ordinary sea water, will develop into normal larvae
without previous fertilization. See PARTHENOGENESIS (artificial).
Again, observation shows that different organisms are adapted to very
diverse environmental conditions, so that what is favourable to one may
be fatal to another. This presumably rests upon a difference in the structural
organization of the protoplasm. But experiment teaches us that an animal
or plant may, by gradually changing the external conditions of life, be
acclimated or accommodated to an environment which would have been fatal
to it before. This change in the conditions of life may be brought about
in a race by natural selection, or it may be produced in an individual
by the direct influence of the environment upon the living matter. Davenport
explains the latter case by the assumption of a specific kind of molecule
in the protoplasm which is capable of responding to a certain stimulus.
The repeated application of this stimulus might destroy these molecules
faster than they could be replaced, and in consequence the organism would
in the end be unable to respond to this particular stimulus. If the stimulus
is an injurious one, the organism would no longer be injured by it. This
hypothesis would explain, not only acclimatization, but also immunity after
inoculations, &c.
Many attempts have been made to localize the various vital processes
within the cell. Thus, the chromatin of the nucleus is regarded by many
as the specific bearer of heredity. It is, however, impossible wholly to
exclude the participation of the cytoplasm in the process of fertilization.
The nucleus, moreover, is sometimes spoken of as the source of the chemical
energy of the cell, though it is more correctly described as the centre
of the metabolic activities of the cell. The nucleus is sometimes seen
to migrate in a large cell to the point of most active growth, and in other
cases is enlarged and curiously modified in correlation with special metabolic
functions of its cell. It is well known that non-nucleated bits of protoplasm,
while they may ingest and partially digest food, are incapable of assimilating
it, and hence soon perish. On the other hand, experiments show that the
nucleus is also incapable of prolonged life without the cytoplasm. It has
also been shown that, though nucleated bits of protoplasm are in many different
organisms capable of regenerating the whole body, nevertheless there is
a limit of size (which differs in different animals) below which such regenerations
cannot occur, on account of deficient organization, even though all the
other conditions seem to be fulfilled. Thus, Lillie found that a nucleated
fragment of the protozoan Stentor could regenerate the whole body, provided
it contained at least one twenty-seventh of the mass of the normal Stentor,
but not if smaller than this.
The reactions of organisms to external stimuli are reduced in last analysis
to reactions of their individual cells; they can therefore best be studied
in the unicellular animals and plants, since here each cell can express
its proper reaction by free movement. Accordingly, we have an extensive
series of researches upon the reactions of such cells to external stimuli,
giving us the following types of simple responsive movements: (1) chemotaxis,
response to chemical stimuli; (2) phototaxis (heliotropism), response to
luminous stimuli; (3) thermotaxis, response to thermal stimuli; (4) hydrotaxis,
movements towards or from moisture; (5) barotaxis, movements determined
by pressure, and including (a) thigmotaxis (strereotaxis), movements
towards or from a solid object; (b) rheotaxis, movements with reference
to the direction of flow of a current of liquid; (c) geotaxis, movements
with reference to the direction of gravity; (6) tonotaxis, movements with
reference to the density of the medium; (7) galvanotaxis (electrotaxis),
movements with reference to electrical stimuli.
It is to be noted that these simple reactions, which are common to animals
and plants, include nearly all (and perhaps quite all) the elements of
the simpler reflexes of higher animals. These reflexes, therefore, as Loeb
has so forcibly argued, are not to be regarded as functions of nerve cells
only, but rather of protoplasm as such.
The preceding reactions may all be described as 'directive effects of
unilateral stimulation' (Verworn). Of course, they are not confined to
unicellular organisms, for free cells within the bodies of higher animals
(leucocytes, sperm cells, &c.) undoubtedly obey these laws; so also
many of the movements of the bodies and organs of these animals, such as
the various tropisms recognized in physiology. Even when free movement
of the reacting cells is prevented by the adjacent tissues, the forces
underlying chemotaxis, &c., undoubtedly govern intra-cellular life
to a large extent. This is best illustrated by the selection of food. Thus,
each of the various types of cells of the body, all of which are bathed
in a common nutrient fluid -- the body lymph -- selects the materials of
which it has need, and no others.
The ultimate explanation of all these reactions is, naturally, to be
sought in internal organization. The importance of the latter factor is
also shown by the fact that the same reaction often follows from very diverse
stimuli. For instance, muscular contraction can be evoked by chemical,
mechanical, thermal, or electrical stimulation. In other words, the organization
of contractile substance is such that if its vital equilibrium is disturbed
by any cause whatever, its energy is discharged in a single mode. It follows
that any living tissue which has any considerable structural differentiation
possesses a certain SPECIFIC ENERGY (q.v.), though just how far the 'specific
energy' of any given organ (notably among the sense organs, where the term
was first applied) is due to internal cellular organization of the primary
reacting cells, and how far to differences in the connections of these
cells with other cells, is still an open question.
Literature: Chemical composition: BUNGE, Lehrb. d. physiol. u.
pathol. Chemie (3rd ed., Leipzig, 1894); GAMGEE, Physiological Chemistry
of the Animal Body (London, 1880); KOSSEL, Ueber die chemische Zusammensetzung
der Zelle, Arch. f. Anat. u. Physiol., Physiol. Abth. (1891); LEA, Chemical
Basis of the Animal Body, Appendix to Foster's Physiol. (6th ed.); MALFATTI,
Zur Chemie des Zellkerns, Ber. d. naturw. -med. Vereins zu Innsbruck, xx
(1891-2); NEUMEISTER, Lehrb. d. physiol. Chemie (2nd ed., Jena, 1897);
PFLÜGER, Ueber die physiologische Verbrennung in den lebendigen Organismen,
Arch. f. d. ges. Physiol., x (1875); REINKE and RODEWALD, Stud. ü.
das Protoplasma (Berlin, 1881); SCHWARZ, Die morphologische und chemische
Zusammensetzung des Protoplasmas, Beitr. z. Biol. d. Pflanzen, v (Breslau,
1887); ZINOFFSKY, Ueber die Grösse des Hämoglobinmolecüls,
Zeitsch. f. physiol. Chemie, x (1885); LOEW, Die chemische Energie der
lebenden Zellen (Munich, 1899); The Proteids of Living Matter, Science,
N.S., xi (1900).
Microscopic structure: R. ALTMANN, Die Elementarorganismen u. ihre Beziehungen
zu den Zellen (2nd ed., Leipzig, 1894); G. F. ANDREWS, The Living Substance
as such and as Organism, J. of Morphol., xii. No. 2, suppl. (1897); TH.
BOVERI, Zellenstudien, Jena. Zeitsch. f. Naturwiss., N. F., xiv (1887),
xv (1888), xvii (1890); O. BÜTSCHLI, Untersuch. ü. mikr. Schäume
u. das Protoplasma (Leipzig, 1892; Eng. trans. with extensive bibliog.,
London, 1894); J. B. CARNOY, A series of articles in La Cellule, i. ff.;
Y. DELAGE, La Structure du Protoplasma et les Théories sur l'Hérédité
(Paris, 1895); T. W. ENGELMANN, Zur Anatomie und Physiologie der Flimmerzellen,
Arch. f. d. ges. Physiol., xxiii (1880); R. v. ERLANGER, Neuere Ansichten
über die Struktur des Protoplasmas, Zool. Centralbl., iii (1896);
W. FLEMMING, Zellsubstanz, Kern u. Zelltheilung (Leipzig, 1882); Neue Beiträge
zur Kenntniss der Zelle, ii. Theil, Arch. f. mikr. Anat., xxxvii (1891);
M. HEIDENHAIN, Ueber Kern und Protoplasma, Festschr. f. Kölliker (1893);
L. F. HENNEGUY, Leçons sur la Cellule (Paris, 1896); O. HERTWIG,
Die Zelle und die Gewebe (Jena, 1892; Eng. trans., The Cell, Outlines of
General Anat. and Physiol., London and New York, 1895); C. NÄGELI,
Mechanisch-physiol. Theorie der Abstammungslehre (Munich and Leipzig, 1884);
E. A. SCHÄFER, On the Structure of Amoeb. Protoplasm, Proc. Roy. Soc.
(London, 1891); E. STRASBURGER, Zellbildung und Zellteilung (3rd ed., Jena,
1880); Stud. ü. das Protoplasma, Jena. Zeitsch. f. Naturwiss., x (1876);
W. WALDEYER, Die neueren Ansichten über den Bau und das Wesen der
Zelle, Deutsch. med. Wochensch. (1895); A. WEISMANN, Essays upon Heredity
and kindred Biol. Problems (trans. from the German; 2 vols., Oxford, 1892);
The Germ-Plasm, a Theory of Heredity (trans., New York, 1893); J. WIESNER,
Die Elementarstruktur u. das Wachstum d. lebenden Substanz (Vienna, 1892);
E. B. WILSON, The Cell in Devel. and Inheritance (New York and London,
1898); The Structure of Protoplasm, in Biol. Lects. delivered at the Marine
Biol. Lab. 1898-9 (Boston, 1899), also in Science, N.S., x, July 14, 1899;
A. ZIMMERMANN, Die Morphologie und Physiologie des pflanzlichen Zellkernes,
eine krit. Litteraturstudie (Jena, 1896).
Properties: BERTHELOT, Fixation directe de l'Azote atmosphérique libre
par certains Terrains argileux, C. R. Acad. d. Sci., ci (1885), cxv (1892),
cxvi (1893); A. BINET, The Psychic Life of Micro-organisms (authorized trans.,
Chicago, 1890); G. BORN, Ueber Verwachsungsversuche mit Amphibienlarven, Arch.
f. Entwicklungsmech., iv (1896); H. BUCHNER, Die chemische Reizbarkeit der Leukocyten,
&c., Sitzber d. Ges. f. Morphol. u. Physiol. z. München, vi (1891);
C. B. DAVENPORT, A Preliminary Catalogue of the Processes concerned in Ontogeny,
Bull. Mus. Compar. Zool., xxvii. 6 (1895); Exper. Morphol., Pt. I (New York
and London, 1897), Pt. II (1899; contains extensive classified bibliographies);
DAVENPORT and CASTLE, On the Acclimatization of Organisms to High Temperatures,
Arch. f. Entwicklungsmech., ii. 2 (1895); DAVENPORT and NEAL, On the Acclimatization
of Organisms to Poisonous Chemical Substances, Arch. f. Entwicklungsmech., ii.
4 (1896); R. DUBOIS, Sur la Perception des Radiations lumineuses par le Peau,
chez les Protées aveugles des Grottes de la Carniole, C. R. Acad. d.
Sci., cx (1890); H. DRIESCH, Heliotropismus bei Hydroïdenpolypen, Zool.
Jahrb., System. Abth., v (1890); Entwicklungsmech. Stud., i-vi, Zeitsch. f.
wiss. Zool. (1891-3); Analytische Theorie d. organischen Entwicklung (Leipzig,
1894); Stud. ü. das Regulationsvermögen d. Organismen, Arch. f. Entwicklungsmech.,
v (1897); TH. EIMER, Die Entstehung der Arten auf Grund von Vererben erworb.
Eigenschaften (Jena, 1888; Eng. trans., London, 1890); T. W. ENGELMANN, Über
Licht-und Farbenperception niederster Organismen, Arch. f. d. ges. Physiol.,
xxix (1882); Bacterium photometricum, ein Beitrag zur vergleichenden Physiologie
des Licht- und Farbensinns, Arch. f. d. ges. Physiol., xxx (1883); Ueber Bewegungen
der Zapfen und Pigmentzellen der Netzhaut, &c., Arch. f. d. ges. Physiol.,
xxxv (1885); R. v. ERLANGER, Die neuesten Ansichten ü. die Zelltheilung
und ihre Mechanik, Zool. Centralbl., iii (1896); L. ERRARA, On the Cause of
Physiological Action at a Distance, Rep. Brit. Assoc. Adv. Sci. (1892); C. W.
HARGITT, Experimental Studies upon Hydromedusae, Biol. Bull., i. I (1899); M.
HEIDENHAIN, Cytomechanische Studien, Arch. f. Entwicklungsmech., i. 4 (1895);
C. HERBST, Ueber die Bedeutung der Reizphysiologie für die kausale Auffassung
von Vorgängen in der tierischen Ontogenese, Biol. Centralbl., xiv-xv (1894-5);
Ueber die zur Entwickelung der Seeigellarven nothwend. anorg. Stoffe, i. Theil,
Arch. f. Entwicklungsmech., v (1897); O. HERTWIG, Ueber den Einfluss der Temperatur
auf die Entwick., Arch. f. mikr. Anat., li (1898); W. E. GARREY, The Effects
of Ions upon the Aggregation of Flagellated Infusoria, Amer. J. of Physiol.,
iii (1900); W. HIS, Unsere Körperform und das physiologische Problem ihrer
Entstehung (Leipzig, 1874); Ueber mechanische Grundvorgänge thierischer
Formenbildung, Arch. f. Anat. u. Physiol., Anat. Abth. (1894); H. S. JENNINGS,
The Psychology of a Protozoon, Amer. J. of Psychol., x. 4 (1899); The Behaviour
of Unicellular Organisms, Woods Holl Biol. Lects. for 1899 (Boston); Studies
on Reactions to Stimuli in Unicellular Organisms -- I. Reactions to Chemical,
Osmotic, and Mechanical Stimuli in the Ciliate Infusoria, J. of Physiol., xxi
(1897); II. The Mechanism of the Motor Reactions of Paramecium, Amer. J. of
Physiol., ii (1899); III. Reactions to Localized Stimuli in Spirostomum and
Stentor, Amer. Natural., xxxiii (1899); IV. Laws of Chemotaxis in Paramecium,
Amer. J. of Physiol., ii (1899); V. On the Movements and Motor Reflexes of the
Flagellata and Ciliata, Amer. J. of Physiol., iii (1900); -- Reactions of Infusoria
to Chemicals, a Criticism, Amer. Natural., xxxiv (1900); P. JENSEN, Ueber den
Geotropismus niederer Organismen, Arch. f. d. ges. Physiol., liii (1893); E.
KORSCHELT, Beiträge zur Morphologie und Physiologie des Zellkerns, Zool.
Jahrb., Abth. f. Anat., iv (1889); F. E. LILLIE, On the Smallest Parts of Stentor
capable of Regeneration, a Contribution on the Limits of Divisibility of Living
Matter, J. of Morphol., xii. I (1896); J. LOEB, Einleitung in die vergleichende
Gehirnphysiologie und vergleichende Psychologie, &c. (Leipzig, 1899; Eng.
trans., 1900); On the Artificial Production of Normal Larvae (Arbacia), Amer.
J. of Physiol., iii. 9 (1900), and Science, N. S., xi. No. 277 (1900); O. LOEW,
Ein natürliches System der Gift-Wirkungen (Munich, 1893); The Energy of
the Living Substance (London, 1896); E. MACH, Beiträge zur Analyse der
Empfindungen (Jena, 1886); Die Principien der Wärmelehre (Leipzig, 1896);
J. MASSART, La Sensibilité à Concentration chez les Êtres
unicellulaires marins, Bull. Acad. Roy. Belg. (3) xxii (1891); Sur l'Irritabilité
des Noctiluques, Bull. Sci. France et Belg., xxv (1893); E. MAUPAS, Sur la Puissance
de Multiplication des Infusoires ciliés, C. R. Acad. d. Sci., civ (1887);
E. METSCHNIKOFF, Leçons sur la Pathologie comparée de l'Inflammation
(Paris, 1892); C.S. MINOT, Senescence and Rejuvenation, J. of Physiol., xii
(1891); T. H. MORGAN, Experimental Studies on Echinoderm Eggs, Anat. Anz., ix.
5, 6 (1893); Studies of the 'Partial' Larvae of Sphaerechinus, Arch. f. Entwicklungsmech.,
ii. I (1895); Half Embryos and Whole Embryos from one of the first two Blastomeres
of the Frog's Egg, Anat. Anz., x. 19 (1895); The Fertilization of Non-nucleated
Fragments of Echinoderm Eggs, Arch. f. Entwicklungsmech., ii. 2 (1895); The
Production of Artificial Astrospheres, Arch. f. Entwicklungsmech., iii (1896);
W. A. NAGEL, Ueber Galvanotaxis, Arch. f. d. ges. Physiol., lix (1895); Der
Lichtsinn augenloser Thiere (Jena, 1896); W. PFEFFER, Ueber chemotakt. Bewegungen,
Untersuch. Bot. Inst. Tübingen, ii (1888); JULIA B. PLATT, On the Specific
Gravity of Spirostomum Paramecium, and the Tadpole, Amer. Natural., xxxiii (1899);
H. QUINCKE, Ueber den Einfluss des Lichtes auf den Thierkörper Arch. f.
d. ges. Physiol., 1vii (1894); A. RAUBER, Ueber den Einfluss der Temperatur,
Sitzber. d. Naturf.-Ges. z. Leipzig, x (1884); W. ROUX, Gesammelte Abhandl.
ü. Entwicklungsmech. d. Organismen (Leipzig, 1895); H. S. RUSSELL, The
Effects of Mechanical Movement, Bot. Gaz., xvii (1892); J. SACHS, Gesammelte
Abhandl. ü. Pflanzenphysiol. (Leipzig, 1892); A. SCHAPER, Experimental
Studies, J. Boston Soc. Med. Sci. (Jan., 1898); Arch. f. Entwicklungsmech.,
vi (1898); O. v. SICHERER, Chemotaxis der Warmblüter-Leukocyten ausserhalb
des Körpers, Münch. med. Wochensch., xliii (1896); E. STRASBURGER,
Wirkung des Lichtes und der Wärme auf Schwärmsporen, Jena. Zeitsch.
f. Naturwiss., xii (1878); H. M. VERNON, The Effect of Environment on the Development
of Echinoderm Larvae, an Experimental Inquiry into the Causes of Variation,
Philos. Trans. Roy. Soc., clxxxvi. B (1895); M. VERWORN, Psychophysiologische
Protistenstudien (Jena, 1889); Allg. Physiol. (Jena, 1897); General Physiology,
an Outline of the Science of Life (Eng. trans., London and New York, 1899; contains
a good bibliography); A. D. WALLER, Galvanotropism of Tadpoles, Sci. Progress,
iv (1895); S. WATASÉ, On the Nature of Cell-Organization, Woods Holl
Biol. Lects., 1893 (Boston); C. O. WHITMAN, The Seat of Formative and Regenerative
Energy, J. of Morphol., ii (1888); The Inadequacy of the Cell-theory of Development,
Woods Holl Biol. Lects., 1893 (Boston); Evolution and Epigenesis, Woods Holl
Biol. Lects., 1894 (Boston); S. R. WILLIAMS, The Specific Gravity of some Fresh-water
Animals in relation to their Habits, Development, and Composition, Amer. Natural.,
xxxiv (1900); S. WINOGRADSKY, Recherches sur les Organismes de la Nitrification,
Ann. d. l'Inst. Pasteur, iv (1890); Recherches sur l'Assimilation, Arch. des
Sci. Biol. de St.-Petersbourg, iii (1895); R. M. YERKES, Reaction of Entomostraca
to Stimulation by Light, Amer. J. of Physiol., iii. 4 (1899); E. YUNG, Contributions
à l'Histoire de l'Influence des Milieux physiques sur les Êtres
vivants, Arch. de Zool., vii (1878), and 2nd series, i (1883); De l'Influence
des Lumières colorées sur le Développement des Animaux,
Mitteil. d. zool. Stat. zu Neapel, ii (1880), and C. R. Acad. d. Sci., cxv (1892);
L. ZENDER, Die Entstehung des Lebens aus mechanischen Grundlagen entwickelt,
Pts. I and II (Tübingen, 1900); O. HERTWIG, Zeit- und Streitfragen der
Biologie (Jena, i. 1894, ii. 1897); E. B. WILSON, Recent Aspects of Biological
Research; Origin of Life and Heredity, Int. Monthly, ii. (1900). (H.H.)
Local Sign: Ger. Lokalzeichen;
Fr. signes locaux; Ital. segni locali. A specific 'shading'
or 'colouring' of certain sensations whereby every such sensation is invariably
referred to a definite position upon the organ or elsewhere in space.
The local signs of pressure may be regarded either as intensive differences
of thickness in the epidermis, differences in tightness of the stretching of
the skin over underlying parts, &c. (Lotze), or as qualitative (Wundt).
The local signs of vision may be simple sensations set up by reflex movements
of ocular rotation (Lotze, Helmholtz), similarity and difference of neighbouring
and remote impressions (Lipps), or complexes of 'movement' sensations and retinal
qualities (see INDIRECT VISION), such as gradations in colour tone (Wundt, Baldwin).
Some sort of local sign is a necessity for theories of space-perception of the
class designated genetic nativism in the article EXTENSION (q.v.). In some cases
localization can be shown, by experiment, to imply the existence of a disparate
local sign: so tactual localization by association with vision. This fact is,
so far, an argument for the existence, in other cases, of a local sign in kind.
See SPACE (perception of), and EXTENSION. (E.B.T.)
This sort of localization should be distinguished from the perception of space
or of extension. See SPACIALIZATION. Specific LOCALIZATION IN SPACE (q.v., I)
may require a local sign independently of or in addition to the data of the
perception of extension, as appears negatively in the vague LOCALIZATION OF
SOUNDS (q.v., also LOCALIZATION IN SPACE, 2). (J.M.B.)
Literature: LOTZE, Med. Psychol. (1852); STUMPF, Ursprung d. Raumvorstellung,
86 ff.; Zeitsch. f. Psychol., iv. 70 ff.; KÜLPE, Outlines of Psychol.,
344, 368 ff.; SANFORD, Course in Exper. Psychol., expt. 1; HELMHOLTZ, Physiol.
Optik (2nd ed.), 670, 947; WUNDT, Physiol. Psychol. (4th ed.), ii. 36 ff., 231
ff.; Human and Animal Psychol., 168 f.; Outlines of Psychol., 105, 127, 134
ff.; LIPPS, Psychol. Stud. (1885), i; Grundthatsachen d. Seelenlebens, 476 f.,
488 ff., 513 ff., 542 ff.; FUNKE, in Hermann's Handb. d. Physiol., III. ii.
404 ff. See also under EXTENSION. (E.B.T.)
Localization (cerebral)
[Lat. locus, place]: Ger. corticale Localisation; Fr. localisations
cérébrales (generally plural); Ital. localizzazioni
funzionali del cervello. (1) The doctrine that various parts of the
brain have relatively distinct functions.
(2) The theory that certain psychical and physiological functions are
limited to definite areas or regions of the brain (especially the distribution
of conscious activities, such as visual, auditory, and other sensations,
as well as voluntary movement of various groups of muscles, to sharply
limited areas of cortex).
The theory in its broadest form is thoroughly substantiated by anatomical,
pathological, and experimental data.
Two distinct tendencies are represented by the schools headed by Ferrier
and Munk on the one hand, and Goltz on the other; the one school claiming
that well-defined areas may be recognized, whose functions are limited
to reactions upon a single set of muscles or a single class of sensory
disturbances, or both; the other laying great emphasis on the unity of
the brain, and the fact that injury to any region affects the whole cortex,
altering the psychical tone as a whole. Munk claims that such motor disturbances
as occur after injury, e.g. to the parietal cortex, depend upon an impairment
of the sensations necessary to the release of such movements.
Probably the two views are not necessarily antagonistic when properly
interpreted. It may be granted that certain areas of cortex actually stand
primarily related to certain groups of muscles (or their myelonic centres),
and certain other areas receive the stimuli elaborated in the primary projection
centre for one organ of special sense; but it may still be true that every
mental presentation is a result of a process of equilibration in the entire
organ, and thus that a localized injury will express itself in alterations
of mental tone rather than a simple abolition of a single kind of mental
expression or a specific modification of consciousness.
The undoubted fact of substitutional functioning is not difficult to
understand in view of the great complexity of the cortex, and especially
of the far-reaching inter-communication of its different regions.
The precise and minute delimitation of the motor and sensory areas is
of great practical importance as an aid in diagnosis and operation in intra-cranial
injuries; but it has much less significance for the proper construction
of metal processes than has sometimes been supposed.
Our most reliable data are derived from experimental study of lower
animals and records of autopsies in cases of brain trauma. Naturally the
results of complete extirpation of the hemispheres have not been observed
in man. In a few instances such an operation has succeeded in dogs, with
results such as the following: strong irritation of the skin caused the
animal to growl and bite, loud noises awakened him from sleep, taste of
food excited impulse to eat, and he reacted to some extent to visual stimuli.
On the other hand, originative power was destroyed and all trace of recognition
and memory was obliterated. In other words, although complicated cyclical
reflexes exist, there is no evidence of psychic functions of the higher
orders. All voluntary motion is, of course, impossible.
The researches of Munk have proved the very minute delimitation of the
motor areas for the limbs and body regions, and also for the special senses.
The centrifugal paths from the various parts of the cortical field for
vision are said to be arranged to correspond quite minutely with the parts
representing the various parts of the retina, so that visual stimuli give
rise to co-ordinated oculo-motor reflexes appropriate to direct the axes
of vision towards the segment of the retina stimulated, and experimental
irritation of these cortical regions calls out the same reflexes -- the
subject not being under the influence of an anaesthetic.
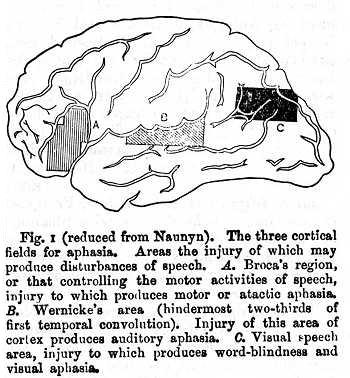
Removal of a single cortical motor centre, or the cortical centres
for both limbs on one side, results in the permanent prevention of all
independent voluntary motions of the corresponding muscles, but such motions
as are performed in common with other organs, especially those of the corresponding
muscles of the other side, may still be performed. So walking, swimming,
and co-ordinated motions may coexist with a true cortical hemiplegia, thus
showing that the volitional stimulus for correlated motions passes via
a secondary apparatus below the cortex. The arrangement explains the possibility
of an acquired quasi-reflex mechanism. The areas for general sensation
correspond in general to the cortical motor areas for the same regions,
though the two are not mutually inclusive. The reported loss of sensation
due to operative injury of the hippocampal region and limbic lobe is probably
due to simultaneous injury of corona fibres which here lie near the surface.
While removal of the cortical areas for the extremities destroys permanently
the tactile sensations for the corresponding members, the general sensitiveness
remains, as also the response to painful irritation. The localized tactile
sense is abolished, while general sensation and pain are simply modified
or diminished.
The explanation of the facts of localization is attended with difficulties,
but it is rendered simpler by recent histological researches (see BRAIN,
and NERVOUS SYSTEM). Munk refers the loss of motor and sensory power resulting
from extirpation of the cortical areas to the prevention of the formation
of the motor and sensory presentations. A dog whose visual sphere is removed
may then be said to suffer psychical blindness, and it would be but a step
to add that the motor inco-or-dination resulting from injuries to the centres
for the extremities is a psychical paralysis (cf. PSYCHIC DUMBNESS). The
minute delimitation of the areas for each segment of a sensory field is
rendered impossible by the overlapping and intercommunication between them,
but there is no reason to doubt the existence of such extensive representation
on the cortex. The most recent experiments all confirm the idea that the
entire cortical representative apparatus reacts as a single mechanism,
so that every 'state of consciousness' is in a sense the product of the
equilibration of the totality of cortical activities. The preponderance
of activity in one sensory sphere affects this rapport, in a way
constituting a conscious excitation of that sense. It follows that any
injury to one part of that cortex not only abolishes the vestiges of previous
excitations of that sense, but enfeebles the entire intelligence, by cutting
out a variety of associational vestiges, both of the lost sense excitations
and of presentations in which they formed an essential part, though originating
in other spheres.
Details of localization may be gathered from the figures.
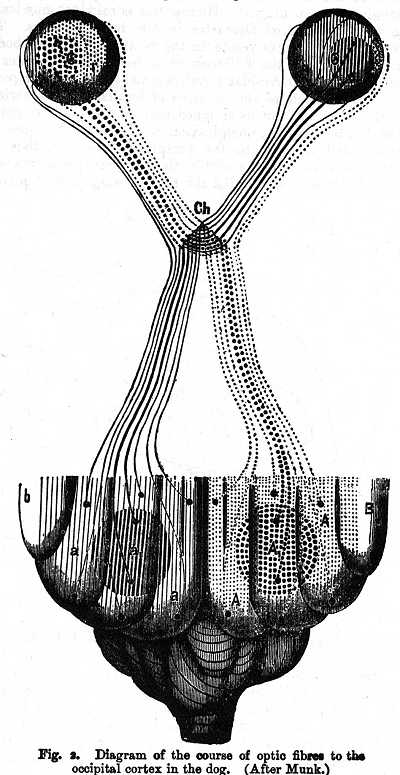
Historical. That the brain is in some way associated with thought
was recognized very early, and this view prevailed among the Greek physicians,
in spite of the fact that Aristotle described the brain as the most bloodless
and inert organ of the body, designed simply to regulate the heat of the
latter, much as the condensing vapours of the sky mitigate summer heat
and drought. Pythagoras, Hippocrates, and Plato clearly recognized the
head as the seat of the intellect and will, while in the days of Ptolemy
Soter some attempt was made to localize functions. Erasistratus believed
that the sensory nerves spring from the meninges, while the motor are derived
from the substance of the brain itself (a view intelligible when we take
into account the close attachment of the sensory ganglia to the meninges).
Hierophilus is said to have anticipated Descartes in the belief that the
vital forces reside in the ventricles, a view to which the followers of
Galen also subscribed. The Arabian physicians and their successors extended
the doctrine of localization. Albertus Magnus assigned judgment to the
frontal regions, imagination to the parietal, and memory to the occipital.
The notion of animal spirits within the ventricles survived to some extent
till the 18th century. Malpighi was the first to ascribe the higher functions
to the grey matter.
Descartes was the first to elaborate a consistent theory of brain functioning.
Influenced by Harvey's discovery of the mechanics of circulation, he taught
that the friction involved in circulation sufficed to vaporize and excite
various elements of the blood. Some of these elements pass to the reproductive
organs, and behave as the forerunners of Darwin's gemmules might be expected
to do, while others, destined to the brain, there evolve the gaseous animal
spirits on which nervous action depends. All nerves are tubes containing
these spirits. In the sensory nerves the currents set towards the brain,
where the agitation is communicated to the central mass of vital fluids
therein. The currents thus produced may, under suitable conditions, pass
out through the motor nerves to muscles, producing what are now called
reflexes. The soul itself is lodged in the 'pineal body,' which was selected
from among the organs of the body because of its central azygous position
and its close connection with the ventricles. The soul is usually affected
by the currents setting from the body, and fabricates its presentations
from the impression thus derived, but it also impresses its own acts upon
the vital fluids, giving rise to motor currents. Aimless eddies may produce
phantasy, and there is a separate mental activity to correspond to each
form of disturbance in the vital humours.
Descartes' speculations prepared the way for a variety of localization
theories. Willis located memory in the convolutions, imagination in the
callosum, sense-perception in the striatum, visual perception in the thalamus,
and involuntary motion in the cerebellum. Meyer, on the other hand, regarded
the cerebellum as the organ of abstraction, and located memory in the roots
of the cranial nerves. Thus the way was prepared for Gall and Spurzheim.
Gall's theory rested on the assumption that the skull depends for its form
upon the growing brain, that therefore its surface reflects the state of
development of the brain, and that size and configuration alone determine
mental power. To these may be added sundry crude psychological postulates.
Though phrenology is primarily a system of psychology, its popularity depended
on the purely empirical form in which it was clothed, while what really
gave it its power with the masses was the fact that it served to give a
scientific character to certain theories which survived astrology under
the name of physiognomy or cheiromancy.
The researches of Broca, by which he was enabled, in 1861, to locate
a cortical centre for articulate speech, mark the real beginning of the
modern doctrine of cortical localization. For a time all disturbances of
speech were referred to this area. Our present knowledge permits us to
state that lesions of the posterior portion, or pars opercularis,
of the third frontal gyrus (commonly known as Broca's convolution, marked
'speech' on Fig. 3) produce motor aphasia, called 'Broca's type,' but many
hold that it is amnesic aphasia, the pure motor aphasia arising from a
subcortical lesion. The accidental discovery by Fritsch and Hitzig, during
the Franco-Prussian War, that the galvanic current applied to the cortex
is capable of exciting the motor mechanism, opened the way for experimental
researches, and from this time onward the pathological method and the experimental
have co-operated in the cultivation of this field. For details of localization
in the case of speech, see SPEECH AND ITS DEFECTS.
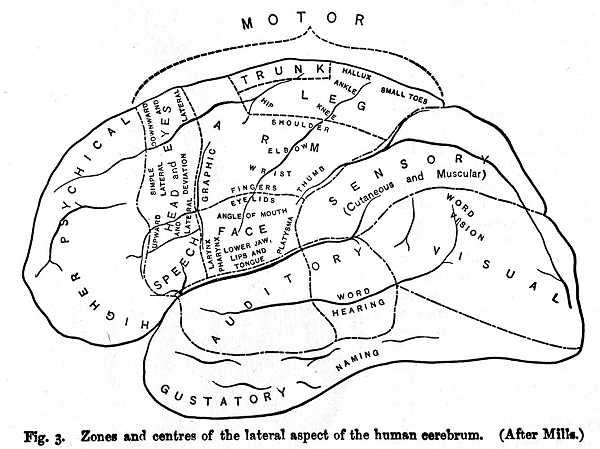 Literature: besides the general treatment in the various physiological
psychologies, the following special memoirs may be consulted: BEEVOR and HORSLEY,
A Minute Analysis of Cortical Centres in the Monkey, Philos. Trans. Roy. Soc.
(1887, 1888); also Arrangement of the Excitable Fibres of the Internal Capsule
of the Bonnet Monkey, Philos. Trans. Roy. Soc. (1890, B); BROCA, Sur le Siège
de la Faculté du Langage articulé, &c. ) Paris, 1861); J.
M. CHARCOT and A. PITRES, Les Centres moteurs corticaux chez l'Homme (Paris,
1895); H. H. DONALDSON, Report of Six Lectures on Cerebral Localization, Amer.
J. of Psychol. iv (1891); L. F. BARKER, The Sense-areas and Association-centres
in the Brain, as described by Flechsig, J. of Nerv. and Ment. Dis., xxiv (June
6, 1897); L. EDINGER, The Significance of the Cortex considered in connection
with a Report upon a Dog from which the whole Cerebrum had been removed by Professor
Goltz, J. of Compar. Neurol., iii (June, 1893); EXNER, Untersuch. ü die
Localisation d. Functionen in d. Grosshirnrinde des Menschen (1884); FERRIER,
The Functions of the Brain (1876); FLOURENS, Recherches expérimentales
sur les Propriétés et les Fonctions du Syst. nerv. (1824); FRITSCH
and HITZIG, Ueber die electrische Erregbarkeit des Grosshirns (1870); GOLTZ,
in Pflüger's Arch. (1876-84), various articles; HERRICK, Neurology and
Psychology, J. of Compar. Neurol., i (1891); HORSLEY and SCHÄFER, A Review
of Experiments upon the Functions of the Cerebral Cortex, Philos. Trans. Roy.
Soc. (1888); LONGET, Anat. et Physiol. du Syst. nerv. (1842); LUCIANI and SEPPILLI,
Die Functions-Localisation auf der Grosshirnrinde (Leipzig, 1886), trans. of
the original, issued as a prize paper by the R. Ist. Lombardo di Scienze e Lettere
(1885); LUCIANI and TAMBURINI, Sulle Funzioni del Cervello, Centri psicomotorii
e Centri psicosensorii, Riv. Sperim. di Freniat. (1878-9); LUCIANI, Sulle Funzioni
del Cervelletto, Riv. Freniat. (1879); and II Cervelletto, Pubblicaz. del R.
Istituto sup. (Firenze, 1891); MAGENDIE, Leçons sur la Fonction du Syst.
nerv. (1884); C. K. MILLS, Cortial Localization in the Light of Recent Researches
into the Minute Anatomy of the Cortex, J. of Nerv. and Ment. Dis., N.S., xx
(1895); also Cerebral Localization in the Light of Recent Pathological Researches,
J. of Amer. Med. Assoc., xxvi (1896), and The Nerv. Syst. and its Diseases (Philadelphia,
1898); MUNK, Ueber die Functionen der Grosshirnrinde, Gesammelte Mittheilungen
(2nd ed., Berlin, 1890); Ueber die Fühlsphären der Grosshirnrinde,
Sitzber. kgl. preuss. Akad. zu Berlin (1892 ff.); Ueber den Hund ohne Grosshirn,
Arch. f. Anat. u. Physiol., Physiol. Abth. (1894); NOTHNAGEL and NAUNYN, Ueber
die Localisation d. Gehirnkrankheiten (1887); J. SOURG, Le Syst. nerv. central
(1899); A. TAMBURINI, Contrib. alla Fisiol. e Patol. del Linguaggio, Riv. Freniat.
(1875); VULPIAN, Leçons de Physiol. du Syst. nerv. (1866). (H.H.)
Literature: besides the general treatment in the various physiological
psychologies, the following special memoirs may be consulted: BEEVOR and HORSLEY,
A Minute Analysis of Cortical Centres in the Monkey, Philos. Trans. Roy. Soc.
(1887, 1888); also Arrangement of the Excitable Fibres of the Internal Capsule
of the Bonnet Monkey, Philos. Trans. Roy. Soc. (1890, B); BROCA, Sur le Siège
de la Faculté du Langage articulé, &c. ) Paris, 1861); J.
M. CHARCOT and A. PITRES, Les Centres moteurs corticaux chez l'Homme (Paris,
1895); H. H. DONALDSON, Report of Six Lectures on Cerebral Localization, Amer.
J. of Psychol. iv (1891); L. F. BARKER, The Sense-areas and Association-centres
in the Brain, as described by Flechsig, J. of Nerv. and Ment. Dis., xxiv (June
6, 1897); L. EDINGER, The Significance of the Cortex considered in connection
with a Report upon a Dog from which the whole Cerebrum had been removed by Professor
Goltz, J. of Compar. Neurol., iii (June, 1893); EXNER, Untersuch. ü die
Localisation d. Functionen in d. Grosshirnrinde des Menschen (1884); FERRIER,
The Functions of the Brain (1876); FLOURENS, Recherches expérimentales
sur les Propriétés et les Fonctions du Syst. nerv. (1824); FRITSCH
and HITZIG, Ueber die electrische Erregbarkeit des Grosshirns (1870); GOLTZ,
in Pflüger's Arch. (1876-84), various articles; HERRICK, Neurology and
Psychology, J. of Compar. Neurol., i (1891); HORSLEY and SCHÄFER, A Review
of Experiments upon the Functions of the Cerebral Cortex, Philos. Trans. Roy.
Soc. (1888); LONGET, Anat. et Physiol. du Syst. nerv. (1842); LUCIANI and SEPPILLI,
Die Functions-Localisation auf der Grosshirnrinde (Leipzig, 1886), trans. of
the original, issued as a prize paper by the R. Ist. Lombardo di Scienze e Lettere
(1885); LUCIANI and TAMBURINI, Sulle Funzioni del Cervello, Centri psicomotorii
e Centri psicosensorii, Riv. Sperim. di Freniat. (1878-9); LUCIANI, Sulle Funzioni
del Cervelletto, Riv. Freniat. (1879); and II Cervelletto, Pubblicaz. del R.
Istituto sup. (Firenze, 1891); MAGENDIE, Leçons sur la Fonction du Syst.
nerv. (1884); C. K. MILLS, Cortial Localization in the Light of Recent Researches
into the Minute Anatomy of the Cortex, J. of Nerv. and Ment. Dis., N.S., xx
(1895); also Cerebral Localization in the Light of Recent Pathological Researches,
J. of Amer. Med. Assoc., xxvi (1896), and The Nerv. Syst. and its Diseases (Philadelphia,
1898); MUNK, Ueber die Functionen der Grosshirnrinde, Gesammelte Mittheilungen
(2nd ed., Berlin, 1890); Ueber die Fühlsphären der Grosshirnrinde,
Sitzber. kgl. preuss. Akad. zu Berlin (1892 ff.); Ueber den Hund ohne Grosshirn,
Arch. f. Anat. u. Physiol., Physiol. Abth. (1894); NOTHNAGEL and NAUNYN, Ueber
die Localisation d. Gehirnkrankheiten (1887); J. SOURG, Le Syst. nerv. central
(1899); A. TAMBURINI, Contrib. alla Fisiol. e Patol. del Linguaggio, Riv. Freniat.
(1875); VULPIAN, Leçons de Physiol. du Syst. nerv. (1866). (H.H.)
Localization (in space).
Localization in space is the reference of a sense impression or of an object
to a local position.
The two general questions which should be distinguished are those (1)
of the distribution of localities on the area of the skin and retina (see
LOCAL SIGN), together with the nervous PROJECTION (q.v.) of sensations
as such to the surface of the body; and (2) the locating of objects in
the external world. See SPACIALIZATION.
The earliest theory of space localization in the sense of (1) is what
Hamilton calls 'the common dogma of the schools, that the soul is all in
the whole body, and all in every one of its parts' (Reid's Works,
Suppl. Diss., 861, note). Then follows the doctrine of Descartes, that
the soul immediately perceives the images in the corporeal phantasy, viz.
the brain. The modern treatment of the subject may be said to start with
Herbart in Germany and with Bain in England.
Literature: for the Herbartian view see VOLKMANN, Lehrb. d. Psychol.,
ii. 117-26; and for Bain's view see BAIN, The Senses and the Intellect, 415
ff. Cf. the textbooks of psychology. See also EXTENSION, and SPACE (perception
of). (G.F.S.- J.M.B.)
Localization (in time).
The reference by the subject of an event in his own history to its position
in the time series relatively to the present moment and to other events,
past and future. See TIME.
The question of the conditions of time localization is comparatively
modern. Its detailed treatment begins with the Herbartian psychology in
Germany. For something of the theory see TEMPORAL SIGN.
Literature: VOLKMANN, Lehrb. d. Psychol., ii. 11-20. There is little
written on the subject by the classical English psychologists; see, however,
JAMES MILL, Analysis, chap. x. The best modern reference in English is, perhaps,
WARD, art. Psychology, Encyc. Brit., 64-5. See the textbooks of psychology.
(G.F.S.- J.M.B.)
Localization of Sounds: Ger. Lokalisation
der Gehörsempfindungen; Fr. localisation des sensations auditives;
Ital. localizzazione (or projezione) spaziale delle sensazioni
uditive. The reference of sounds to particular localities in space. See
SPACIALIZATION. (J.M.B.)
Our apprehension of the distance and direction of sounds appears to
be conditioned, primarily, by the relative intensity of the waves that
reach the two ears. Localization of sounds is thus a function of BINAURAL
HEARING (q.v.). It is doubtful how far the pure auditory perception could
have developed without visual perception; and, indeed, no explanation has
as yet been proposed that is adequate in detail to the observed phenomena.
Literature: PREYER, Pflüger's Arch., xl; VON KRIES, Zeitsch. f.
Psychol., i. 235, 488; MÜNSTERBERG, Beitr. z. exper. Psychol., ii, and
(with PIERCE) Psychol. Rev., i. 461; RAYLEIGH, Nature, xiv. 32; SANFORD, Course
in Exper. Psychol., expts. 101-3; MATSUMOTO, Yale Studies, v. 1 ff.; SCRIPTURE,
ibid., 76 ff.; ANGELL and FITE, Psychol. Rev., viii. 225. (E.B.T.)
Localized Industry: Ger. Weltwirthschaft,
localisirte
Industrie; Fr. spécialisation (d'industrie)
locale;
Ital. industria locale specializzata. The division of labour between
different communities.
'We may mark off three stages of industrial development. The first is where
the distinction of trades is introduced, and men no longer consume all or perhaps
any part of the articles they have produced; yet where consumers live near the
producer and are personally known to him. The second stage is where the element
of personal acquaintance disappears. Production no longer waits for orders,
but anticipates demand. The third stage is reached when increasing facilities
of communication make the world one trading community. Then the localization
of trades proceeds so far that one country, or perhaps one group of towns, produces
the greater part of all the goods of a certain sort that are consumed throughout
the world' (Walker). (A.T.H.)
Locke, John. (1632-1704.) Born at Wrington,
Somersetshire, England, he was educated at Westminster School, London,
and Christ Church, Oxford. Secretary to Sir Walter Vane at Berlin, &c.,
1665-6; formed the acquaintance of Ashley, afterwards Earl of Shaftesbury,
1666. He entered Lord Ashley's family, directing the education of his son
and grandson. As lord chancellor, Shaftesbury made him 'secretary of presentations'
to benefices. He stayed in France and Italy, 1675-9, and in Holland, 1684-9.
In 1690 he published his famous 'Essay,' and died at Oates in Essex, Oct.
28, 1704. He is founder of English EMPIRICISM (q.v., also SENSATIONALISM).
Locomotion (1) and (2)
Locomotor [Lat. locus, place, + motio, a moving]: Ger.
(1) Locomotion, (2) Bewegungs- (werkzeug, &c.); Fr.
locomotion, locomoteur; Ital. (1) locomozione, (2) locomotore.
(1) The act or power of moving from place to place. (2) Pertaining to the mechanism
of locomotion. See MOVEMENT, and MUSCLE. (C.F.H.)
